OBMEP - Olimpíada Brasileira de Matemática das Escolas Públicas
QUESTÃO 01
(OBMEP) Nas balanças da figura, objetos iguais têm pesos iguais. Qual dos objetos é o mais pesado?
GABARITO.
QUESTÃO 02
(OBMEP) A área da figura azul é igual à soma das áreas de quantos quadradinhos do quadriculado?
A) 12
B) 22
C) 32
D) 64
E) 100
GABARITO.
QUESTÃO 03
(OBMEP) Na figura, quantos quadradinhos brancos ainda devem ser pintados de preto para que o número total de quadradinhos pretos passe a ser o dobro do número de quadradinhos brancos?
A) 9
B) 10
C) 11
D) 12
E) 13
GABARITO.
QUESTÃO 04
(OBMEP) Vânia preencheu os quadradinhos da conta abaixo com os algarismos 1, 2, 3, 4, 5, 6, 7 e 8. Ela usou todos os algarismos e obteve o maior resultado possível. Qual foi esse resultado?
A) 402
B) 609
C) 618
D) 816
E) 876
GABARITO.
QUESTÃO 05
(OBMEP) O gráfico de barras mostra a distribuição dos alunos de uma escola conforme o tempo diário dedicado à leitura.
Qual é o gráfico de setores que melhor representa, em amarelo, a fração de alunos que dedicam à leitura no máximo 40 minutos por dia?
GABARITO.
QUESTÃO 06
(OBMEP) Na rede de distribuição de água representada abaixo, a água passa pelos canos como indicado pelas setas e se distribui igualmente em cada ramificação. Em uma hora passaram 200 mil litros de água pela saída X. Quantos litros de água passaram pela saída Y nessa mesma hora?
A) 100 mil litros
B) 130 mil litros
C) 300 mil litros
D) 450 mil litros
E) 600 mil litros
GABARITO.
QUESTÃO 07
(OBMEP) A figura mostra um quadrado de centro O e área 20 cm². O ponto M é o ponto médio de um dos lados. Qual é a área da região sombreada?
A) 6 cm²
B) 6,5 cm²
C) 7 cm²
D) 7,5 cm²
E) 8 cm²
GABARITO.
QUESTÃO 08
(OBMEP) Vários quadrados foram dispostos um ao lado do outro, em ordem crescente de tamanho, formando uma figura com 100 cm de base. O lado do maior quadrado mede 20 cm. Qual é o perímetro (medida do contorno em vermelho) da figura formada por esses quadrados?
A) 220 cm
B) 240 cm
C) 260 cm
D) 300 cm
E) 400 cm
GABARITO.
QUESTÃO 09
(OBMEP) Ana, Beatriz, Carolina, Diana e Elaine, em roda, brincam de falar números consecutivos. Ana começa falando 1, depois Beatriz fala 2 e assim por diante, conforme ilustrado na fi gura. Elas iniciam a brincadeira no sentido horário e mudam o sentido toda vez que o número falado for múltiplo de 7.
Qual delas vai falar o número 32?
A) Ana
B) Beatriz
C) Carolina
D) Diana
E) Elaine
GABARITO.
QUESTÃO 10
(OBMEP) Em uma mesa há nove cartões numerados de 1 a 9. Ana e Beto pegaram três cartões cada um. A soma dos números dos cartões de Ana é 7 e a soma dos números dos cartões de Beto é 23. Qual é a diferença entre o maior e o menor dos números dos três cartões deixados sobre a mesa?
A) 3
B) 4
C) 5
D) 6
E) 7
GABARITO.
QUESTÃO 11
(OBMEP) Para obter tinta de cor laranja, devem-se misturar 3 partes de tinta vermelha com 2 partes de tinta amarela. Para obter tinta de cor verde, devem-se misturar 2 partes de tinta azul com 1 parte de tinta amarela. Para obter tinta de cor marrom, deve-se misturar a mesma quantidade de tintas laranja e verde.
Quantos litros de tinta amarela são necessários para obter 30 litros de tinta marrom?
A) 7
B) 8
C) 9
D) 10
E) 11
GABARITO.
QUESTÃO 12
(OBMEP) Uma roda-gigante está parada com o banco 8 na posição mais baixa e o banco 3 na posição mais alta.
Seus bancos estão igualmente espaçados e numerados em ordem a partir do número 1. Quantos bancos tem essa roda-gigante?
A) 8
B) 10
C) 12
D) 14
E) 16
GABARITO.
QUESTÃO 13
(OBMEP) Em um dos lados de uma folha de papel grosso, Pedro desenhou a figura ao lado. Depois, recortou-a e montou uma torre em miniatura.
Das cinco imagens abaixo, quais podem representar a torre montada por Pedro?
A) Imagens 1, 3 e 5
B) Imagens 1, 4 e 5
C) Imagens 1, 2 e 3
D) Imagens 2, 3 e 4
E) Imagens 3, 4 e 5
GABARITO.
QUESTÃO 14
(OBMEP) Mônica e seu namorado foram assistir a uma peça de teatro. O auditório era organizado em fileiras paralelas ao palco, todas com o mesmo número de cadeiras dispostas lado a lado.
Eles se sentaram um ao lado do outro nos dois últimos lugares vagos. Mônica percebeu que havia, no total, 14 pessoas nas fileiras à sua frente e 21 pessoas nas fi leiras atrás da sua.
Quantas cadeiras havia no auditório?
A) 37
B) 38
C) 40
D) 42
E) 49
GABARITO.
QUESTÃO 15
(OBMEP) Na conta armada, cada letra representa um algarismo, e letras diferentes representam algarismos diferentes. Qual é o algarismo que a letra T representa?
A) 0
B) 1
C) 3
D) 5
E) 7
GABARITO.
QUESTÃO 16
(OBMEP) Zequinha tem três dados iguais, com letras O, P, Q, R, S e T em suas faces. Ele juntou esses dados como na figura, de modo que as faces em contato tivessem a mesma letra. Qual é a letra na face oposta à que tem a letra T?
A) S
B) R
C) Q
D) P
E) O
GABARITO.
QUESTÃO 17
(OBMEP) Após digitar um número de seis algarismos em sua calculadora, Cecília observou que dois algarismos 9 que ela havia digitado não apareceram no visor; o que apareceu foi 2017. Quantas são as possibilidades para o número que ela digitou?
A) 6
B) 9
C) 10
D) 15
E) 18
GABARITO.
QUESTÃO 18
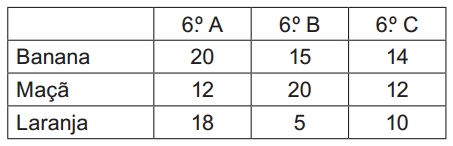
(OBMEP) Uma escola fez uma pesquisa com todos os alunos do sexto ano para verificar se eles gostavam de banana, maçã ou laranja. Cada aluno assinalou pelo menos uma dessas três frutas.
A tabela abaixo apresenta os resultados da pesquisa.
Por exemplo, 20 alunos do 6.º A assinalaram que gostam de banana. Quantos alunos há, no mínimo e no máximo, no sexto ano dessa escola?
A) No mínimo 54 e no máximo 126 alunos.
B) No mínimo 54 e no máximo 58 alunos.
C) No mínimo 27 e no máximo 54 alunos.
D) No mínimo 27 e no máximo 126 alunos.
E) No mínimo 31 e no máximo 58 alunos.
GABARITO.
QUESTÃO 19
(OBMEP) Em uma competição, as partidas têm duração de 60 minutos, e cada time tem sempre 5 jogadores em campo. Em determinada partida, um time inscreveu 8 atletas e foram feitas várias substituições de modo que cada um deles jogou a mesma quantidade de tempo.
Quanto tempo cada um deles jogou nessa partida?
A) 27 minutos e 30 segundos
B) 30 minutos
C) 37 minutos e 30 segundos
D) 40 minutos
E) 42 minutos e 30 segundos
GABARITO.
QUESTÃO 20
(OBMEP) Uma caixa contém 10 bolas verdes, 10 bolas amarelas, 10 bolas azuis e 10 bolas vermelhas.
Joãozinho quer retirar uma certa quantidade de bolas dessa caixa, sem olhar, para ter a certeza de que, entre elas, haja um grupo de sete bolas com três cores diferentes, sendo três bolas de uma cor, duas bolas de uma segunda cor e duas bolas de uma terceira cor.
Qual é o número mínimo de bolas que Joãozinho deve retirar da caixa?
A) 11
B) 14
C) 21
D) 22
E) 23
GABARITO.
NÍVEL 2
QUESTÃO 21
(OBMEP) Dentro de três sacolas idênticas foram colocados objetos de pesos a, b, e c, como na figura. Com isso, o peso da sacola 1 ficou menor que o peso da sacola 2, que por sua vez ficou menor que o peso da sacola 3.
Qual das desigualdades abaixo é verdadeira?
A) a < b < c
B) a < c < b
C) b < a < c
D) b < c < a
E) c < a < b
GABARITO.
QUESTÃO 22
(OBMEP) Na sequência 1, 5, 4, −1, -5, ... cada termo, a partir do segundo, é igual à soma de seus dois vizinhos; por exemplo: 5 = 1 + 4, 4 = 5 + (-1) e -1 = 4 + (-5). Qual é a soma dos 1000 primeiros termos dessa sequência?
A) 0
B) 1
C) 4
D) 9
E) 10
GABARITO.
QUESTÃO 23
(OBMEP) Um ponto está a 1 cm de uma figura quando a menor distância desse ponto aos pontos da figura é 1 cm. Celinha traçou com uma caneta vermelha todos os pontos que estão a 1 cm de distância do círculo da Figura 1. A seguir, ela fez o mesmo para a região quadrada da Figura 2.
Qual é o desenho que ela vai obter se traçar todos os pontos que estão a 1 cm de distância da região poligonal da Figura 3?
GABARITO.
QUESTÃO 24
(OBMEP) João formou um cubo 5 x 5 x 5 usando cubinhos menores numerados, sendo que cada cubinho recebeu um número diferente dos demais. O cubo foi montado de tal modo que a soma dos números em qualquer bloco de 5 cubinhos alinhados lado a lado fosse sempre a mesma. A soma dos números de todos os cubinhos é 7875.
Qual é a soma dos números dos cubinhos de uma face qualquer do cubo?
A) 315
B) 1575
C) 2875
D) 5625
E) 7875
GABARITO.
QUESTÃO 25
(OBMEP) Com pentágonos regulares com 1 cm de lado, formamos uma sequência de polígonos como na figura. O perímetro do primeiro polígono é 5 cm, o perímetro do segundo é 8 cm, e assim por diante.
Quantos pentágonos são necessários para formar um polígono com perímetro igual a 1736 cm?
A) 570
B) 572
C) 574
D) 576
E) 578
GABARITO.
QUESTÃO 26
(OBMEP) José gosta de inventar operações matemáticas entre dois números naturais. Ele inventou uma operação ∎ em que o resultado é a soma dos números seguida de tantos zeros quanto for o resultado dessa soma. Por exemplo,
Quantos zeros há no resultado da multiplicação abaixo?
A) 5
B) 10
C) 14
D) 16
E) 18
GABARITO.
QUESTÃO 27
(OBMEP) Um livro, com páginas numeradas em sequência, está dividido em três capítulos. Cada um dos capítulos tem a mesma quantidade de páginas. A primeira página do Capítulo 1 tem o número 1. A soma do número da primeira página do Capítulo 2 com o número da primeira página do Capítulo 3 é 1052.
Qual é o número da primeira página do Capítulo 3?
A) 699
B) 700
C) 701
D) 702
E) 703
GABARITO.
QUESTÃO 28
(OBMEP) Ana, Bruna, Carla, Débora e Eliane escolheram números de 1 a 100 para participar de um sorteio:
• Ana escolheu o número 5;
• Bruna escolheu o número 15;
• Carla escolheu o número 40;
• Débora escolheu o número 70;
• Eliane escolheu o número 90.
No sorteio, uma bolinha é retirada ao acaso de uma caixa com cem bolinhas numeradas de 1 a 100. Ganhará quem tiver escolhido o número mais próximo do sorteado; em caso de empate, ganhará quem tiver escolhido o maior número.
Qual das meninas tem maior chance de ganhar o sorteio?
A) Ana
B) Bruna
C) Carla
D) Débora
E) Eliane
GABARITO.
QUESTÃO 29
(OBMEP) De quantas maneiras diferentes é possível pintar de preto algumas casas do quadriculado abaixo de modo que, em cada linha e em cada coluna, fiquem pintadas de preto exatamente três casas?
A) 4
B) 6
C) 16
D) 24
E) 32
GABARITO.
QUESTÃO 30
(OBMEP) Na figura, dois vértices do hexágono regular maior coincidem com dois vértices do hexágono regular menor. O hexágono menor tem área igual a 10 cm². Qual é a área do hexágono maior?
A) 20 cm²
B) 30 cm²
C) 35 cm²
D) 36 cm²
E) 40 cm²
GABARITO.
QUESTÃO 31
(OBMEP) Na figura vemos um quadrado dentro de outro, determinando uma região cinza. A área (em cm²) e o perímetro (em cm) dessa região são numericamente iguais, ou seja, o valor numérico da soma dos perímetros desses quadrados é igual ao valor numérico da diferença entre suas áreas. Qual é a diferença entre as medidas dos lados desses quadrados?
A) 1 cm
B) 4 cm
C) 6 cm
D) 8 cm
E) 10 cm
GABARITO.
QUESTÃO 32
(OBMEP) Pelo centro do quadrado da Figura 1 traçam-se duas retas perpendiculares, que o dividem em quatro quadriláteros iguais. Esses quadriláteros são rearranjados em outro quadrado maior, como na Figura 2. Qual é a área do quadrado ABCD da Figura 2?
A) 16 cm²
B) 25 cm²
C) 36 cm²
D) 49 cm²
E) 64 cm²
GABARITO.
QUESTÃO 33
(OBMEP) Em uma festa havia somente 3 mulheres, e 99% dos convidados eram homens. Quantos homens devem deixar a festa para que a porcentagem de homens passe a ser igual a 98% do total de participantes?
A) 3
B) 30
C) 100
D) 150
E) 297
GABARITO.
QUESTÃO 34
(OBMEP) Qual é o valor da expressão abaixo?
A) 4
B) 5
C) 6
D) 7
E) 8
GABARITO.
QUESTÃO 35
(OBMEP) Sérgio quer numerar de 1 a 16 os triângulos da Figura 1 de tal modo que números consecutivos fiquem em triângulos que têm um lado comum. Por exemplo, ele pode numerar os triângulos como na Figura 2.
De quantas maneiras Sérgio pode fazer isso?
A) 16
B) 32
C) 48
D) 56
E) 64
GABARITO.
NÍVEL 3
QUESTÃO 36
(OBMEP) Na figura abaixo, D, E e F são pontos médios dos lados do triângulo ABC, e G, H e I são pontos médios dos lados do triângulo FBE. A área do triângulo ABC é 48 cm². Qual é a área da região destacada em amarelo?
A) 16 cm²
B) 18 cm²
C) 20 cm²
D) 22 cm²
E) 24 cm²
GABARITO.
QUESTÃO 37
(OBMEP) Se a − b = 1 e ab = 1, qual é o valor de a² + b²?
A) 1
B) 2
C) 3
D) 4
E) 5
GABARITO.
QUESTÃO 38
(OBMEP) Ana, Beatriz e Cristina treinam numa pista de corrida. Ana corre sempre com o dobro da velocidade de Beatriz e com o triplo da velocidade de Cristina.
Um dia, Ana partiu do fim da pista, correndo em sentido contrário ao de suas amigas, no mesmo instante em que Beatriz e Cristina partiram do início da pista.
Após o treino, Ana disse para suas amigas que tinha percorrido 20 metros desde o momento em que cruzou com Beatriz até o momento em que cruzou com Cristina.
Quantos metros tem a pista?
A) 200 metros
B) 220 metros
C) 240 metros
D) 300 metros
E) 360 metros
GABARITO.
QUESTÃO 39
(OBMEP) Somando 1 a um certo número natural, obtemos um múltiplo de 11. Subtraindo 1 desse mesmo número, obtemos um múltiplo de 8. Qual é o resto da divisão do quadrado desse número por 88?
A) 0
B) 1
C) 8
D) 10
E) 80
GABARITO.
QUESTÃO 40
(OBMEP) Se f(x) = 5x² + ax + b, com a ≠ b, f(a) = b e f(b) = a, qual é o valor de a + b?

GABARITO.
QUESTÃO 41
(OBMEP) Na figura, o arco AC é um quarto de uma circunferência de centro D e o arco AB é um oitavo de uma circunferência de centro C. O segmento AD mede 2 cm. Qual é a área em cm² da região verde?
A) 2
B) π
C) 4
D) 2π
E) 4π
GABARITO.
QUESTÃO 42
(OBMEP) A maior potência de 2 que divide o produto 1 × 2 × ∙∙∙ × 2023 × 2024 é 2²⁰¹⁷. Qual é a maior potência de 2 que divide o produto 1 × 2 × ∙∙∙ × 4047 × 4048?
A) 2²⁰¹⁸
B) 2⁴⁰³⁴
C) 2⁴⁰⁴¹
D) 2⁶⁰⁵¹
E) 2⁸⁰⁶⁸
GABARITO.
QUESTÃO 43
(OBMEP) No interior do quadrado ABCD de lado 9 cm, foram traçadas as semicircunferências de centros E, F e G, tangentes como indicado na figura. Qual é a medida de AG?

GABARITO.
QUESTÃO 44
(OBMEP) Por duas vezes Benício juntou, como na figura, três dados com faces numeradas de 1 a 6, de tal modo que faces em contato tivessem o mesmo número. Em cada uma das vezes ele somou os números de todas as faces que não ficaram em contato entre si.
A diferença entre as somas obtidas foi 16. Quais são os números das faces que nunca ficaram em contato entre si?
A) 1 e 4
B) 1 e 6
C) 2 e 5
D) 3 e 4
E) 2 e 6
GABARITO.
QUESTÃO 45
(OBMEP) Na figura, os ângulos
 e
e medem 120°, o ângulo
medem 120°, o ângulo é reto, e os segmentos BC e CD medem 4 cm e 8 cm, respectivamente. Qual é a área do quadrilátero ABCD em cm²?
é reto, e os segmentos BC e CD medem 4 cm e 8 cm, respectivamente. Qual é a área do quadrilátero ABCD em cm²?A) 14√3
B) 28√3
C) 32√3
D) 36√3
E) 40√3
GABARITO.
QUESTÃO 46
(OBMEP) Na figura abaixo, BHEG é um retângulo com BG > BH, e A, C, D, F são pontos médios de seus respectivos lados. Um ponto P desloca-se ao longo da poligonal ABCDEF, partindo de A até o ponto F.
Qual é o gráfico que melhor representa a área R(x) do triângulo APF em função da distância x percorrida pelo ponto P ao longo dessa poligonal?
GABARITO.
QUESTÃO 47
(OBMEP) João tem 148 copos dispostos em fila, cada um contendo um grão de feijão. Em etapas, João reduz a quantidade de copos da fila da seguinte maneira:
• se em uma etapa a quantidade de copos for par, ele coloca os feijões do último copo no primeiro, do penúltimo no segundo, do antepenúltimo no terceiro e assim por diante, descartando os copos vazios;
• se em uma etapa a quantidade de copos for ímpar, ele coloca os feijões do último copo no segundo, do penúltimo no terceiro, do antepenúltimo no quarto e assim por diante, também descartando os copos vazios.
Quando a fila se reduzir a dois copos, quantos feijões estarão no primeiro copo?
A) 4
B) 10
C) 16
D) 20
E) 36
GABARITO.
QUESTÃO 48
(OBMEP) Ana e Beto foram os únicos candidatos na eleição para a presidência do grêmio estudantil da escola em que ambos estudam. Nessa eleição, votaram ao todo 1450 alunos.
Durante a apuração, houve um momento em que Ana teve a certeza de que, ao fi nal, ela teria pelo menos a metade dos votos válidos. Naquele momento, os percentuais eram os seguintes:
• votos não válidos: 20% dos votos apurados;
• votos em Ana: 60% dos votos válidos;
• votos em Beto: 40% dos votos válidos.
Quantos votos tinham sido apurados até aquele momento?
A) 1110
B) 1150
C) 1200
D) 1250
E) 1300
GABARITO.
QUESTÃO 49
(OBMEP) Para quantos conjuntos {a, b, c} de três números naturais é verdade que a × b × c = 2310?
A) 24
B) 30
C) 32
D) 36
E) 40
GABARITO.
QUESTÃO 50
(OBMEP) Uma caixa contém nove bolas idênticas numeradas de 1 a 9. Uma primeira bola é sorteada, seu número é anotado e a bola é devolvida à caixa. Repete-se esse procedimento mais duas vezes, anotando-se também os números da segunda e terceira bolas sorteadas.
Qual é a probabilidade de que a soma dos números nas duas primeiras bolas sorteadas não seja um múltiplo de 3 e a soma dos números nas três bolas sorteadas seja um múltiplo de 3?

GABARITO.
FONTE: https://www.indagacao.com.br/2019/06/questoes-obmep-com-gabarito-e-resolucao.html










































Comentários