Exercícios de Física 1º ano Ensino Médio com Respostas

Exercícios de Física Ensino Médio com Respostas
 

1. Um macaco que pula de galho em galho em um zoológico, demora 6 segundos para atravessar sua jaula, que mede 12 metros. Qual a velocidade média dele?

S=12m

t=6s

v=?

2. Um carro viaja de uma cidade A a uma cidade B, distantes 200km. Seu percurso demora 4 horas, pois decorrida uma hora de viagem, o pneu dianteiro esquerdo furou e precisou ser trocado, levando 1 hora e 20 minutos do tempo total gasto. Qual foi a velocidade média que o carro desenvolveu durante a viagem?

S=200km

t=4h

v=?

Mesmo o carro tendo ficado parado algum tempo durante a viagem, para o cálculo da velocidade média não levamos isso em consideração.

3. No exercício anterior, qual foi a velocidade nos intervalos antes e depois de o pneu furar? Sabendo que o incidente ocorreu quando faltavam 115 km para chegar à cidade B.

• Antes da parada:

S= 200-115=85km

t=1hora

v=?

• Depois da parada:

S= 115km

t= 4h-1h-1h20min= 1h40min=1,66h (utilizando-se regra de três simples)

v=?

4. Um bola de basebol é lançada com velocidade igual a 108m/s, e leva 0,6 segundo para chegar ao rebatedor. Supondo que a bola se desloque com velocidade constante. Qual a distância entre o arremessador e o rebatedor?

, se isolarmos S:

5. Durante uma corrida de 100 metros rasos, um competidor se desloca com velocidade média de 5m/s. Quanto tempo ele demora para completar o percurso?

, se isolarmos t:

Movimento Uniforme:

1. Um carro desloca-se em uma trajetória retilínea descrita pela função S=20+5t (no SI). Determine:

(a) a posição inicial;

(b) a velocidade;

(c) a posição no instante 4s;

(d) o espaço percorrido após 8s;

(e) o instante em que o carro passa pela posição 80m;

(f) o instante em que o carro passa pela posição 20m.

Comparando com a função padrão: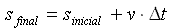 

(a) Posição inicial= 20m

(b) Velocidade= 5m/s

(c) S= 20+5t

S= 20+5.4

S= 40m

(d) S= 20+5.8

S= 60m

(e) 80= 20+5t

80-20=5t

60=5t

12s =t

(f) 20= 20+5t

20-20= 5t

t=0

2. Em um trecho de declive de 10km, a velocidade máxima permitida é de 70km/h. Suponha que um carro inicie este trecho com velocidade igual a máxima permitida, ao mesmo tempo em que uma bicicleta o faz com velocidade igual a 30km/h. Qual a distância entre o carro e a bicicleta quando o carro completar o trajeto?

• Carro:

S=10km

v=70km/h

t=?

S=70t

10=70t

0,14h=t

t=8,57min (usando regra de três simples)

• Bicicleta

O tempo usado para o cálculo da distância alcançada pela bicicleta, é o tempo em que o carro chegou ao final do trajeto: t=0,14h

v=30km/h

t=0,14h

S=?

S=0+30.(0,14)

S=4,28Km

3. O gráfico a seguir mostra as posições em função do tempo de dois ônibus. Um parte de uma cidade A em direção a uma cidade B, e o outro da cidade B para a cidade A. As distâncias são medidas a partir da cidade A. A que distância os ônibus vão se encontrar?

Para que seja possível fazer este cálculo, precisamos saber a velocidade de algum dos dois ônibus, e depois, calcular a distância percorrida até o momento em que acontece o encontro dos dois, onde as trajetórias se cruzam.

Calculando a velocidade ônibus que sai da cidade A em direção a cidade B (linha azul)

Sabendo a velocidade, é possível calcular a posição do encontro, quando t=3h.

4. Um carro, se desloca a uma velocidade de 20m/s em um primeiro momento, logo após passa a se deslocar com velocidade igual a 40m/s, assim como mostra o gráfico abaixo. Qual foi o distância percorrida pelo carro?

Tendo o gráfico da v x t, o deslocamento é igual à área sob a reta da velocidade. Então:

S= Área A + Área B

S=205 + 40(15-5)

S=100+400

S=500m

5. Dois trens partem simultaneamente de um mesmo local e percorrem a mesma trajetória retilínea com velocidades, respectivamente, iguais a 300km/h e 250km/h. Há comunicação entre os dois trens se a distância entre eles não ultrapassar 10km. Depois de quanto tempo após a saída os trens perderão a comunicação via rádio?

Para este cálculo estabelece-se a velocidade relativa entre os trens, assim pode-se calcular o movimento como se o trem mais rápido estivesse se movendo com velocidade igual a 50km/h (300km/h-250km/h) e o outro parado.

Assim:

v=50km/h

S=10km

t=?

1. A distância média entre a Terra e o Sol é de 150.000.000 km. Quanto tempo a luz demora para chegar à Terra? (Considerando c = 300.000 km/s).

O primeiro passo é entender o deslocamento da luz. Como c é uma velocidade constante, o movimento deve ser uniforme, ou seja:

Com isto, basta substituir os valores dados no exercício:

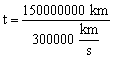
Ainda podemos expressar este tempo em minutos:

Portanto, a luz demora aproximadamente 8 minutos e 20 segundos para viajar do Sol até a Terra.

2. Quando as missões espaciais chegaram à Lua foram deixados espelhos em sua superfície para que pudessem ser feitos experimentos com eles. Suponhamos que, usando um destes espelhos, você deseje descobrir a distância entre a Terra e a Lua. É usado, então, um feixe de laser que é captado após 2,54 segundos. Desconsiderando os movimentos da Terra e da Lua, e usando c = 300.000 km/s, qual a distância entre o nosso planeta e o seu satélite natural?

Como no exercício anterior, a luz descreve um movimento uniforme, logo:

O tempo necessário para que o laser atinja os receptores é equivalente à viagem de ida e volta da luz, logo, precisamos usar a metade deste tempo, ou seja, 1,27 segundos:

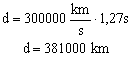
3. Ano-luz é a medida de distância usada em astronomia que se refere ao espaço percorrido pela luz durante um ano terrestre. Considerando c = 300.000 km/s e 1 ano = 365,25 dias, quantos quilômetros equivale a um ano-luz?

Precisamos converter a unidade de tempo para segundos e, para isso, precisamos saber que:

1 minuto = 60 segundos

1 hora = 60 minutos = 3600 segundos

1 dia = 24 horas = 1440 minutos = 86400 segundos

1 ano = 8766 horas = 525960 minutos = 31557600 segundos

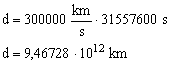
1. (UFPB 2005) Um pesquisador realiza uma experiência envolvendo as grandezas: Força, Distância e Tempo, para obter o valor de uma outra grandeza física. Se a dimensão da grandeza obtida é massa × (comprimento)²/(tempo)³, então a sua unidade no sistema internacional (MKS) é

a) watt
b) joule
c) newton
d) kilograma x metro / segundo
e) newton /metro


2. (UFPB 2005) Quando um trem de metrô vai de uma estação A até uma estação B, distantes 1800 m, ele acelera (na saída) e desacelera (na chegada) na mesma razão de 2 m/s². Sabendose que, por questões de segurança, o trem não pode ultrapassar a velocidade de 30 m/s (108 km/h), então o gráfico que melhor representa a velocidade do trem em função do tempo é:

a) 
b) 
c) 
d) 
e) 


3. (UFPB 2005) Uma pista de brinquedo, inteiramente contida num plano vertical, tem o formato mostrado na figura abaixo. Um carrinho em repouso é largado no ponto A e inicia o seu movimento de descida acelerado pela força gravitacional.



Considerando-se que os pontos A e C estão na mesma altura e que não há atrito entre a pista e o carrinho, pode-se afirmar que este carrinho

a) perderá contato com a pista no ponto B.
b) perderá contato com a pista entre os pontos B e C.
c) perderá contato com a pista no ponto C.
d) perderá contato com a pista entre os pontos C e D.
e) não perderá contato com a pista.


4. (UFPB 2005) Um bloco de 1 kg está apoiado sobre uma prancha de 4 kg, como mostra a figura. O bloco é puxado por uma força F horizontal. Os coeficientes de atrito estático e dinâmico entre o bloco e a prancha são 0,8 e 0,6, respectivamente.



Considerando-se que o atrito entre a prancha e o solo é desprezível, então é correto afirmar que a maior aceleração da prancha será:

a) 1,0 m/s²
b) 1,2 m/s²
c) 1,5 m/s²
d) 1,6 m/s²
e) 2,0 m/s²


5. (UFPB 2005) Um bloco de 1 kg colide com uma mola de constante elástica 2 N/m, como mostra a figura.



O coeficiente de atrito dinâmico entre o bloco e o solo é 0,1. Observando-se que a compressão máxima da mola foi 1 m, então conclui-se que a velocidade do bloco no instante da colisão era

a) 0,5 m/s
b) 1,0 m/s
c) 1,5 m/s
d) 2,0 m/s
e) 2,5 m/s


6. (UFPB 2005) A figura mostra um trapezista, prestes a executar o seu famoso salto “quíntuplo mortal”, no instante em que a amplitude de seu movimento pendular é máxima. A diferença entre as posições mais alta e mais baixa alcançadas pelo centro de massa do trapezista é 3 m. O trapezista tem 50 kg e a distância entre o seu centro de massa e o suporte que prende os cabos do trapézio é 10 m.



Nesse contexto, conclui-se que a tensão em cada um dos dois cabos do trapézio, no ponto mais baixo da trajetória, vale:

a) 200 N
b) 300 N
c) 400 N
d) 500 N
e) 600 N


7. (UFPB 2005) Um projétil é disparado com velocidade v contra um bloco de madeira, inicialmente em repouso, sobre uma superfície sem atrito. O projétil atravessa o bloco e emerge com velocidade v/10. Se a massa do bloco é 1000 vezes maior que a massa do projétil, então a velocidade adquirida pelo bloco é:

a) 10^-2 v
b) 10^-3 v
c) 9 x 10^-4 v
d) 9 x 10^-5 v
e) 9 x 10^-6 v


8. (UFPB 2005) O gráfico mostra a variação das velocidades com o tempo de dois blocos que colidem ao longo da direção x.



Nesse contexto, é correto afirmar:

a) A colisão é perfeitamente elástica.
b) A colisão é perfeitamente inelástica.
c) Os blocos movimentam-se sempre no mesmo sentido.
d) A relação entre as massas é m₂ = 3m₁.
e) A relação entre as massas é m₂ = m₁.


9. (UFPB 2007) Considere os vetores A, B e F, nos diagramas numerados de I a IV.



Os diagramas que, corretamente, representam a relação vetorial F = A – B são apenas:

a) I e III
b) II e IV
c) II e III
d) III e IV
e) I e IV


10. (UFPB 2007) A distância aproximada, entre João Pessoa e Campina Grande, é de 120km. Um ciclista deseja fazer esse percurso em sua bicicleta que, a cada pedalada, percorre 60cm. O número de pedaladas necessárias, para fazer o percurso, é aproximadamente:

a) 1,2 x 10⁴
b) 2,0 x 10⁴
c) 1,2 x 10⁵
d) 2,0 x 10⁵
e) 1,2 x 10⁶


11. (UFPB 2007) Uma partícula em movimento retilíneo tem sua velocidade, em função do tempo, representada no gráfico abaixo.



De acordo com o gráfico, o instante de tempo no qual a partícula retorna à posição inicial, correspondente a t=0, é:

a) 3 s
b) 6 s
c) 9 s
d) 12 s
e) 15 s


12. (UFPB 2007) Um bloco encontra-se sobre uma mesa horizontal sob a ação de uma força F. Compare as situações esboçadas abaixo, em que o módulo de F é sempre o mesmo, mas sua direção varia.



Com relação ao módulo da força normal (N) exercida pela mesa sobre o bloco, é correto afirmar que

a) N_II > N_I > N_III
b) N_I > N_II > N_III
c) N_II > N_III > N_I
d) N_III > N_II > N_I
e) N_I > N_III > N_II


13. (UFPB 2007) Dois blocos A e B de massas m_A = 6 kg e m_B = 4 kg, respectivamente, estão apoiados sobre uma mesa horizontal e movem-se sob a ação de uma força F de módulo 60N, conforme representação na figura abaixo.



Considere que o coeficiente de atrito dinâmico entre o corpo A e a mesa é m_A = 0,2 e que o coeficiente entre o corpo B e a mesa é m_B = 0,3. Com base nesses dados, o módulo da força exercida pelo bloco A sobre o bloco B é:

a) 26,4 N
b) 28,5 N
c) 32,4 N
d) 39,2 N
e) 48,4 N


14. (UFPB 2007) Um esquiador desliza sem atrito por uma pista de esqui, mostrada na figura a seguir, sob a ação apenas da gravidade. Ele parte do repouso do ponto A e passa pelos pontos B e C, mantendo sempre o contato com a pista.



Os valores das energias mecânica (E), cinética (K) e potencial (U) do esquiador são representados por colunas verticais, em que o comprimento da parte sombreada é proporcional a esses valores. Com base nessas informações, analise os diagramas numerados de I a VI.



Os diagramas que melhor representam a distribuição energética, nos pontos A, B e C, respectivamente, são:

a) I, IV e V
b) II, IV e VI
c) II, III e V
d) I, II e III
e) I, II e V


15. (UFPB 2007) Uma força horizontal, constante e de intensidade 20N, atua sobre um corpo de 10 kg de massa, inicialmente em repouso, que desliza sem atrito sobre uma superfície horizontal. A potência média transmitida ao corpo, ao longo dos primeiros 100 m, é

a) 500 W
b) 300 W
c) 100 W
d) 400 W
e) 200 W


16. (UFPB 2007) Dois corpos, A e B, de massas m_A = 3 kg e m_B = 2 kg, respectivamente, deslocam-se sem atrito sobre um plano horizontal. Inicialmente, seus vetores velocidade são v_A = 3i + 2j e v_B = –2i + 3j, onde i e j são, respectivamente, os vetores unitários, nas direções x e y, de um sistema cartesiano sobre o plano. Os valores das componentes são dados em m/s. Em um dado instante, os corpos colidem e o corpo A tem sua velocidade alterada para v′_A = i + 3j.
Nessas circunstâncias, o novo vetor velocidade do corpo B é: 

a) v′_B = 1,5i+2j
b) v′_B = i+2j
c) v′_B = 2i+1,5j
d) v′_B = i+1,5j
e) v′_B = 1,5i–2j


17. (UFPB 2007) Em uma conferência pela internet, um meteorologista brasileiro conversa com três outros colegas em diferentes locais do planeta. Na conversa, cada um relata a temperatura em seus respectivos locais. Dessa forma, o brasileiro fica sabendo que, naquele momento, a temperatura em Nova Iorque é T_NI=33,8^oF, em Londres, T_L=269^oK, e em Sidnei, T_S=27^oC. Comparando essas temperaturas, verifica-se:

a) T_NI>T_S>T_L
b) T_NI>T_L>T_S
c) T_L>T_S>T_NI
d) T_S>T_NI>T_L
e) T_S>T_L>T_NI


18. (UFPB 2007) Os materiais utilizados na construção civil são escolhidos por sua resistência a tensões, durabilidade e propriedades térmicas como a dilatação, entre outras. Rebites de metal (pinos de formato cilíndrico), de coeficiente de dilatação linear 9,8 × 10^–6oC^–1, devem ser colocados em furos circulares de uma chapa de outro metal, de coeficiente de dilatação linear 2,0 × 10^–5oC^–1. Considere que, à temperatura ambiente (27^oC), a área transversal de cada rebite é 1,00cm² e a de cada furo, 0,99cm². A colocação dos rebites, na chapa metálica, somente será possível se ambos forem aquecidos até, no mínimo, a temperatura comum de:

a) 327 ^oC
b) 427 ^oC
c) 527 ^oC
d) 627 ^oC
e) 727 ^oC


19. (UFPB 2007) Numa indústria de engarrafamento e liquefação de gases, um engenheiro lida, freqüentemente, com variações na pressão e no volume de um gás devido a alterações de temperatura. Um gás ideal, sob pressão de 1atm e temperatura ambiente (27^oC), tem um volume V. Quando a temperatura é elevada para 327^oC, o seu volume aumenta em 100%. Nessa situação, a pressão do gás, em atm, é:

a) 0,5
b) 1,0
c) 1,5
d) 2,0
e) 2,5


20. (UFPB 2007) Um engenheiro testa materiais para serem usados na fabricação da carroceria de um automóvel. Entre outras propriedades, é desejável a utilização de materiais com alto calor específico. Ele verifica que, para aumentar em 3oC a temperatura de 32g do material A, é necessário fornecer 24cal de calor a esse material. Para obter o mesmo aumento de temperatura em 40g do material B, é preciso 24cal. Já 50g do material C necessitam 15cal para sofrer o mesmo acréscimo de temperatura. Os calores específicos dos materiais A, B e C são respectivamente:

a) c_A = 0,25cal/g^oC ; c_B = 0,20cal/g^oC ; c_C = 0,10cal/g^oC
b) c_A = 0,20cal/g^oC ; c_B = 0,35cal/g^oC ; c_C = 0,15cal/g^oC
c) c_A = 0,30cal/g^oC ; c_B = 0,10cal/g^oC ; c_C = 0,20cal/g^oC
d) c_A = 0,35cal/g^oC ; c_B = 0,20cal/g^oC ; c_C = 0,10cal/g^oC
e) c_A = 0,10cal/g^oC ; c_B = 0,30cal/g^oC ; c_C = 0,25cal/g^oC


21. (UFPB 2007) Um Professor de Física utiliza uma mola, de constante elástica k e comprimento L (quando não distendida), para demonstrar em sala de aula o movimento harmônico simples (MHS). A mola, presa ao teto da sala, pende verticalmente. Um corpo de massa m é preso à extremidade livre da mola e subitamente largado. Desprezando todas as forças dissipativas, admitindo que a mola tem massa desprezível e que a gravidade terrestre é g , analise as afirmações a seguir:

I. O período do MHS obtido é T = 2p(L/g)^1/2.
II. O corpo não realiza MHS devido à gravidade.
III. A nova posição de equilíbrio está deslocada de DL = mg/k.
IV. A energia mecânica total do corpo, no movimento vertical, é igual à soma das suas energias cinética, potencial elástica e potencial gravitacional.

Estão corretas apenas:

a) I e II
b) I e III
c) I e IV
d) II e III
e) III e IV


22. (UFPB 2007) Uma das cordas de uma harpa tem comprimento igual a 50cm. O maior comprimento de onda estacionária que um músico pode estabelecer nessa corda, em cm, é:

a) 12,5
b) 25
c) 50
d) 100
e) 200


23. (UFPB 2007) Em um experimento de óptica, em sala de aula, uma régua de 30,0cm de comprimento, quando colocada perpendicular ao eixo principal e a 24,0cm do vértice de um espelho esférico côncavo, produz uma imagem invertida de 10,0cm de altura. Nessas circunstâncias, a distância focal do espelho, em cm, é:

a) 2
b) 3
c) 4
d) 5
e) 6


24. (UFPB 2007) Um mergulhador de uma equipe de resgate submarino está debaixo da água e usa sua lanterna à prova d’água, para sinalizar à equipe de apoio (fora da água) que pode içar a carga a ser resgatada. Os diagramas, a seguir, representam a passagem de um raio de luz da água para o ar, a ângulos de incidência diferentes.



De acordo com a Lei de Snell de refração de luz, os diagramas que correspondem a situações físicas realistas são apenas:

a) I e II
b) I e III
c) I, III e IV
d) II e III
e) II e IV


25. (UFPB 2006) Um cidadão está à procura de uma festa. Ele parte de uma praça, com a informação de que o endereço procurado estaria situado a 2km ao norte. Após chegar ao referido local, ele recebe nova informação de que deveria se deslocar 4km para o leste. Não encontrando ainda o endereço, o cidadão pede informação a outra pessoa, que diz estar a festa acontecendo a 5km ao sul daquele ponto. Seguindo essa dica, ele finalmente chega ao evento. Na situação descrita, o módulo do vetor deslocamento do cidadão, da praça até o destino final, é:

a) 11 km
b) 7 km
c) 5 km
d) 4 km
e) 3 km


26. (UFPB 2006) Uma partícula é abandonada de uma altura h em relação ao solo. Durante a queda, além da aceleração da gravidade, essa partícula fica sujeita a uma aceleração horizontal constante devido a uma força horizontal que atua sobre a mesma. Nessas condições, a trajetória da partícula está melhor representada no gráfico:

a) 
b) 
c) 
d) 
e) 


27. (UFPB 2006) Após a ocorrência de um pequeno acidente, um astronauta necessita fazer um reparo na parte externa de sua espaçonave, que possui um formato cilíndrico com um raio de 10m. Ressaltese que a nave espacial está girando em torno de seu próprio eixo, dando uma volta completa a cada 20 segundos, e o astronauta precisa se segurar na mesma para realizar o conserto e não ser lançado no espaço. Para que o astronauta de 70kg se mantenha preso à espaçonave, a força mínima, em newtons, será :

a) 7p²
b) p²
c) p²/10
d) 7p
e) 70


28. (UFPB 2006) Uma locomotiva, desenvolvendo uma aceleração de 2 m/s², puxa três vagões ao longo de uma ferrovia retilínea, conforme a figura.



Se o vagão 3 pesa 2 x 10⁴ N, a força exercida sobre ele pelo vagão 2 é:

a) 4 x 10⁴
b) 1 x 10⁴
c) 1 x 10³
d) 2 x 10³
e) 4 x 10³


29. (UFPB 2006) Três corpos idênticos (1, 2 e 3) são abandonados de uma altura h, com velocidade inicial nula, e chegam ao solo com velocidades v1, v2 e v3, respectivamente. O corpo 1 sofre uma queda livre, enquanto os corpos 2 e 3 deslizam sobre superfícies planas, inclinadas e sem atrito, conforme a figura abaixo.



Considerando a situação descrita, é correto afirmar:

a) v₁ > v₂ > v₃
b) v₁ > v₂ = v₃
c) v₁ = v₂ = v₃
d) v₁ = v₂ > v₃
e) v₁ < v₂ < v₃


30. (UFPB 2006) Um avião decola e segue, inicialmente, uma trajetória de ascensão retilínea por 3km, formando um ângulo de 30º com a horizontal. Se a força gravitacional realizou um trabalho de _1,5 x 10⁸ J, a massa do avião, em toneladas, vale:

a) 10
b) 5
c) 4,5
d) 1,5
e) 1,0


31. (UFPB 2006) Em um caderno de física de um aluno, foram encontradas as afirmativas abaixo sobre colisões entre dois objetos de massa finita. Identifique com V a(s) afirmativa(s) verdadeira(s) e com F, a(s) falsa(s).

( ) A energia cinética é sempre conservada.
( ) A quantidade de movimento é sempre conservada.
( ) As velocidades dos objetos serão sempre iguais , após a colisão, se eles colidirem de forma perfeitamente inelástica.

A seqüência correta é:

a) VVV
b) VVF
c) VFF
d) FVV
e) FFV


32. (UFPB 2006) Há 60 anos, lamentavelmente, foi lançada, sobre Hiroshima, uma bomba atômica cujo princípio físico é o da fissão nuclear. Nesse processo, um núcleo atômico pesado divide-se em núcleos menores, liberando grande quantidade de energia em todas as direções. Suponha que o núcleo de um determinado átomo parte-se em três pedaços de mesma massa, movendo-se com velocidades iguais em módulo (v₁ = v₂ = v₃ = v), nas direções indicadas na figura.
Considere a massa total, após a divisão, igual à massa inicial.



A velocidade v_i do núcleo, antes da divisão, é:

a) 3v
b) 2v
c) v
d) 1/2v
e) 1/3v


33. (UFPB 2007) Dois patinadores, A e B, de massas m_A=60kg e m_B=40kg, respectivamente, estão, inicialmente, juntos e parados em uma pista de gelo. Um dos patinadores empurra o outro, de modo que começam a se afastar. Desprezando o atrito, quando a separação entre eles for 20m, a distância percorrida por cada patinador será respectivamente:

a) X_A = 4m, X_B = 16m
b) X_A = 5m, X_B = 15m
c) X_A = 6m, X_B = 14m
d) X_A = 7m, X_B = 13m
e) X_A = 8m, X_B = 12m


34. (UFPB 2007) Dois satélites idênticos são colocados em órbitas circulares estáveis: um em torno da Terra e o outro em torno de Marte. Como a massa da Terra é, aproximadamente, nove vezes maior que a de Marte e considerando que os satélites descrevem órbitas de raios iguais, a razão entre os períodos dos satélites em torno da Terra e de Marte é:

a) 1/10
b) 1/9
c) 1/6
d) 1/3
e) 1


35. (UFPB 2007) Considere quatro condutores esféricos idênticos (A, B, C e D). Inicialmente, o condutor A está com carga Q_A = 16 C e os outros três, descarregados. Então, o condutor A é colocado em contato com o condutor B; em seguida, coloca-se o condutor A em contato com o condutor C; e, por fim, coloca-se o condutor A em contato com o condutor D. A configuração final de cargas nos quatro condutores é:

a) Q_A = 1C, Q_B = 7 C, Q_C = 6 C, Q_D = 2C
b) Q_A = 2C, Q_B = 8 C, Q_C = 4 C, Q_D = 2C
c) Q_A = 3C, Q_B = 7 C, Q_C = 4 C, Q_D = 2C
d) Q_A = 4C, Q_B = 8 C, Q_C = 2 C, Q_D = 2C
e) Q_A = 5C, Q_B = 7 C, Q_C = 2 C, Q_D = 2C


36. (UFPB 2007) A associação de resistências, representada na figura fica submetida à ação de uma diferença de potencial de 12Volts.



Nesse contexto, considerando que a leitura no amperímetro é 10A, a relação entre as resistências é:

a) R₁ > R₂ > R₃
b) R₂ > R₃ > R₁
c) R₃ > R₁ > R₂
d) R₁ > R₃ > R₂
e) R₂ > R₁ > R₃


37. (UFPB 2007) Duas cargas elétricas puntiformes estão fixadas nos pontos A e B, indicados na figura. Observa-se que o potencial eletrostático é nulo em C (o potencial também é nulo no infinito) e que, nesse ponto, o campo elétrico resultante E tem a direção e o sentido mostrados na figura.



Com essas informações, é possível expressar as cargas elétricas em termos de uma carga q arbitrária e positiva. Assim, as cargas em A e em B são respectivamente:

a) q; –2q
b) 2q; –q
c) –q; q
d) q; –q
e) –2q; q


38. (UFPB 2007) A figura mostra a seção transversal de dois fios longos e paralelos, cada um conduzindo uma corrente de módulo igual a I, mas em sentidos contrários.



Sobre os módulos do campo magnético resultante, B₁, B₂ e B₃, respectivamente, nos pontos P₁, P₂ e P₃, é correto afirmar: 

a) B₁ = mI/(3pd), B₂ = mI/(pd), B₃ = mI/(3pd)
b) B₁ = mI/(2pd), B₂ = mI/(2pd), B₃ = mI/(2pd)
c) B₁ = mI/(3pd), B₂ = mI/(3pd), B₃ = mI/(3pd)
d) B₁ = mI/(4pd), B₂ = mI/(pd), B₃ = mI/(4pd)
e) B₁ = mI/(4pd), B₂ = 0, B₃ = mI/(4pd)


39. (UFPB 2007) Analise as seguintes proposições sobre pressão, identificando as verdadeiras.

(01) A pressão, em um dado ponto no interior de um fluido, depende da área transversal do recipiente naquele ponto.
(02) A pressão aplicada a um fluido é transmitida integralmente a todos os seus pontos e às paredes do recipiente que o contém.
(04) A pressão é uma grandeza física que precisa de módulo, direção e sentido, para ser completamente determinada.
(08) A pressão, em um líquido, aumenta com a profundidade.
(16) A pressão atmosférica não depende da altitude.

A soma dos valores atribuídos às proposições verdadeiras é igual a 


40. (UFPB 2007) Considere um satélite artificial, girando em órbita circular estável ao redor da Terra. Nesse contexto, adotando o referencial em que a energia potencial gravitacional é nula no infinito, identifique, dentre as proposições abaixo, as verdadeiras.

(01) A velocidade do satélite varia com a raiz quadrada da sua massa.
(02) A energia potencial gravitacional do satélite será sempre negativa.
(04) O período do movimento do satélite é proporcional ao cubo do raio.
(08) A energia mecânica total do satélite é sempre positiva.
(16) A velocidade areolar do satélite é sempre constante.

A soma dos valores atribuídos às proposições verdadeiras é igual a 


41. (UFPB 2007) Uma partícula de massa e carga não nulas é lançada em uma região onde existe um campo magnético uniforme. Considerando que a velocidade inicial da partícula é perpendicular ao campo, identifique, dentre as proposições abaixo, as verdadeiras.

(01) O raio da órbita da partícula é diretamente proporcional a sua carga.
(02) O período do movimento da partícula é diretamente proporcional ao raio da sua órbita.
(04) O raio da órbita da partícula é diretamente proporcional a sua massa.
(08) O período do movimento da partícula independe do módulo da velocidade.
(16) O raio da órbita da partícula é inversamente proporcional à intensidade do campo.

A soma dos valores atribuídos às proposições verdadeiras é igual a 


42. (UFPB 2007) Um pai, com 80kg de massa, deseja construir, na sua casa, uma gangorra, para brincar com seu filho pequeno de apenas 20kg de massa. O pai dispõe de uma prancha de madeira resistente de comprimento 2,0m e massa desprezível.



Para que a gangorra fique em equilíbrio (conforme a figura), quando o pai e o filho estiverem sentados, respectivamente, nas extremidades AeB dessa gangorra, a que distância, em cm, da extremidade A, deverá ser colocado o apoio da prancha? 


43. (UFPB 2007) Uma mola, em posição vertical, tem sua extremidade inferior presa ao fundo de um tanque inicialmente vazio. Nessa circunstância, um corpo de massa 2,0kg, quando apoiado na extremidade superior da mola, causa uma compressão de 1,0cm. Quando o tanque estiver cheio com um líquido de densidade 0,8g/cm³, a compressão na mola será de apenas 0,5cm.
Nesse contexto, qual a densidade do corpo, em unidades de 10²kg/m3? 


44. (UFPB 2007) Considere a situação descrita abaixo.

Uma partícula de carga elétrica q=+2×10^–6C e de massa m=1×10^–7kg é liberada, a partir do repouso, em uma região onde existe um campo elétrico uniforme de módulo 5N/C. 

Nessa situação, qual a velocidade da carga, em m/s, após percorrer uma distância de 2m? 


45. (UFPB 2006) Se o diâmetro de uma moeda aumenta 0,2% quando sua temperatura é elevada em 100 ºC, os aumentos percentuais na espessura, na área e no volume serão respectivamente:

a) 0,1 %, 0,2 %, 0,2 %
b) 0,2 %, 0,2 %, 0,2 %
c) 0,2 %, 0,4 %, 0,5 %
d) 0,2 %, 0,4 %, 0,6 %
e) 0,3 %, 0,4 %, 0,8 %


46. (UFPB 2006) Um gás ideal é submetido a três transformações consecutivas, em que A-->B é isobárica, B-->C é isotérmica e C-->A é adiabática, como mostra o diagrama p – V abaixo.



Em relação a essas transformações, identifique com V a(s) afirmativa(s) verdadeira(s) e com F, a(s) falsa(s).

( ) Em A-->B, a energia interna do gás diminui.
( ) Em B-->C, o gás recebe calor.
( ) Em C-->A, não há variação da energia interna do gás.

A seqüência correta é:

a) VVF
b) VFV
c) FVF
d) VVV
e) FFF


47. (UFPB 2006) Antes de iniciar uma viagem, um motorista cuidadoso calibra os pneus de seu carro, que estão à temperatura ambiente de 27 ºC, com uma pressão de 30 lb/pol². Ao final da viagem, para determinar a temperatura dos pneus, o motorista mede a pressão dos mesmos e descobre que esta aumentou para 32 lb/pol². Se o volume dos pneus permanece inalterado e se o gás no interior é ideal, o motorista determinou a temperatura dos pneus como sendo:

a) 17 ^oC
b) 27 ^oC
c) 37 ^oC
d) 47 ^oC
e) 57 ^oC


48. (UFPB 2006) Um bloco de 1 kg, preso a uma mola de constante elástica k= 800 N/m e massa desprezível, oscila sobre um plano horizontal sem atrito com amplitude A=0,5 m. No instante em que a energia cinética do bloco se iguala à energia potencial da mola, a velocidade do bloco vale:

a) 10 m/s
b) 20 m/s
c) 30 m/s
d) 40 m/s
e) 50 m/s


49. (UFPB 2006) Uma partícula material executa um movimento harmônico simples (MHS) em torno do ponto x=0. Sua aceleração, em função da posição, é descrita pelo gráfico abaixo.



Nessas condições, a freqüência angular do MHS é:

a) 4 rd/s
b) 3 rd/s
c) 2 rd/s
d) 1 rd/s
e) 0,5 rd/s


50. (UFPB 2006) A figura abaixo mostra uma corda de densidade linear igual a 1 g/m, que passa por uma roldana. A sua extremidade esquerda está presa a um vibrador e, na extremidade direita, pendura-se um corpo de massa M.



Nessa situação, quando a distância L, entre o vibrador e a roldana, for 0,5 m e a vibração estiver na freqüência de 200 Hz,, a corda vibrará no modo fundamental. Com base nesses dados, o valor de M deve ser igual

a) 3 kg
b) 4 kg
c) 5 kg
d) 6 kg
e) 7 kg


51. (UFPB 2006) Um estudante quer determinar a velocidade da luz em um cubo de material transparente. Para tanto, ele incide luz monocromática no cubo, de acordo com o diagrama abaixo, e mede as distâncias A e B, encontrando A=1 cm e B =  cm.

Dado: Velocidade da luz no ar c =300.000 km/s.

A partir do ângulo de incidência de 60º e dos valores medidos de A e de B, determina-se que a velocidade da luz no meio transparente, para a freqüência utilizada, é:

a) 200.000 km/s
b) 250.000 km/s
c) 300.000 km/s
d) 320.000 km/s
e) 350.000 km/s


52. (UFPB 2006) Nas figuras abaixo, estão representados por “O” os objetos e por “I”, suas respectivas imagens, para lentes convergentes e divergentes. Em cada uma das figuras, identifique com R, quando a imagem for real e com V, quando for virtual.



A seqüência correta é:

a) RRR
b) RRV
c) RVV
d) VVV
e) VVR


53. (UFPB 2004) Enquanto aguarda o seu almoço, uma criança brinca com uma colher, observando a sua imagem no lado convexo da mesma. Considerando-se a colher um espelho esférico, é correto afirmar que a imagem vista pela criança é

a) real, menor e direita.
b) real, menor e invertida.
c) virtual, menor e direita.
d) virtual, maior e direita.
e) virtua l, maior e invertida.


54. (UFPB 2004) Em um dado instante, a forma de uma corda por onde se propaga uma onda é indicada na figura abaixo:



Com base nos dados obtidos da figura e sabendo-se que a velocidade de propagação da onda é de 120 cm/s, pode-se concluir que seu comprimento de onda e freqüência são dados, respectivamente, por:

a) 6 cm e 4 0 Hz
b) 3 cm e 4 0 Hz
c) 9 cm e 1 0 Hz
d) 6 cm e 2 0 Hz
e) 3 cm e 2 0 Hz


55. (UFPB 2004) Numa exibição de “body jumping”, um artista, de massa m, resolve efetuar um salto de demonstração sobre um lago. Querendo provocar grande impressão no público, resolve fazer com que, nesse salto, sua cabeça se aproxime o máximo possível da superfície da água. Para isso, prende-se pelos pés a um fio elástico de massa desprezível e comprimento L, através de um mecanismo que o mantém de cabeça para baixo, ficando esta a uma altura h da água, como mostra a figura.



Dessa posição, o artista deverá ser solto, com velocidade inicial nula. Sendo assim, para que o mesmo apenas encoste suavemente a cabeça na água, a constante elástica do fio, que obedece à lei de Hooke, deve ser no mínimo igual a:

a) mh²/L²
b) mL²/(h -L)²
c) 2mgh/(h-L)²
d) 2mgh/(h+L)²
e) 2mgL/(h+L)²


56. (UFPB 2004) Num dia “frio” de inverno, uma pessoa, em sua casa, desloca-se descalça, da sala para a cozinha. Tratase na verdade de um mesmo ambiente, com os cômodos separados apenas pelo fato de os pisos serem diferentes. O piso da sala é de madeira, enquanto o da cozinha é de cerâmica lisa. Quando ela pisa no chão da cozinha, sente um “frio” intenso em seus pés. Esta sensação ocorreu porque

a) a temperatura da sala é maior do que a da cozinha, uma vez que a cerâmica é mais densa que a madeira.
b) a cerâmica tem uma temperatura menor que a madeira, devido à sua condutividade térmica ser menor.
c) a cerâmica tem maior condutividade térmica, e, portanto, parece mais fria, embora os dois pisos estejam à mesma temperatura.
d) a madeira tem maior condutividade térmica, e, portanto, parece mais quente, embora os dois pisos estejam à mesma temperatura.
e) a cerâmica tem uma temperatura menor que a madeira, uma vez que a sua condutividade térmica é maior.


57. (UFPB 2004) Num laboratório de física, um estudante realiza uma experiência que consiste em variar a pressão e o volume de um gás ideal por três processos diferentes, sendo todos eles entre os mesmos estados i e f, como mostrado nos diagramas p–V abaixo.



Sabendo-se que T’’, T’ e T são isotermas, pode-se concluir que as variações de energia interna (DU₁, DU₂ e DU₃) nos três processos estão na ordem:

a) DU1 > DU2 > DU3
b) DU3 > DU2 > DU1
c) DU2 > DU1 > DU3
d) DU3 > DU1 > DU2
e) DU3 = DU2 = DU1


58. (UFPB 2004) Um garoto brinca com um cilindro que é fechado por um êmbolo em uma de suas extremidades e por uma tampa fixa na outra. O cilindro contém um gás ideal. O garoto inicialmente comprime o êmbolo lentamente, de forma que a temperatura permaneça constante e, posteriormente, com o êmbolo fixado na posição final, deixa-o ao sol para que se aqueça. Em seguida, e ainda com o cilindro ao sol, puxa lentamente o êmbolo, mantendo então a temperatura constante, até o mesmo voltar à posição inicial. Finalmente, deixa o cilindro na sombra, com o êmbolo mantido fixo em sua posição, para que a temperatura do sistema volte ao seu valor inicial. Com base nessas informações, pode-se concluir que o diagrama que melhor representa esse conjunto de transformações é:

a) 
b) 
c) 
d) 
e) 


59. (UFPB 2004) Um professor resolve fazer um teste com uma turma de estudantes e entrega-lhes uma lente escondida dentro de um tubo cilíndrico. As duas extremidades do tubo são fechadas com vidros que não permitem aos estudantes verem a lente em seu interior. No entanto, há no primeiro vidro uma figura que, quando iluminada externamente, produz, no vidro do lado oposto da lente, uma imagem invertida com relação à figura original. Com base nessa informação, os estudantes concluem que a lente é

a) convergente e os vidros estão mais afastados da lente do que seus focos.
b) convergente e os vidros se encontram entre os focos e a lente.
c) divergente e os vidros se encontram mais afastados da lente do que os focos.
d) divergente e a distância desta aos vidros é menor do que a distância focal.
e) convergente e o vidro que contém a figura se encontra entre o foco e a lente. O outro se encontra após o foco.


60. (UFPB 2004) Uma jovem monitora prepara um sistema massamola, como indicado na figura abaixo, com o intuito de fazer uma demonstração para seus estudantes.



A jovem então afasta a massa de seu ponto de equilíbrio, distendendo a mola de uma certa quantidade. A seguir a massa é solta, passando a executar um movimento harmônico simples. Com base nessa situação, pode-se afirmar que o gráfico que melhor representa a variação da energia potencial da massa em função do tempo, a partir do instante em que a jovem a solta, é:

a) 
b) 
c) 
d) 
e) 


61. (UFPB 2004) Num laboratório de física, um estudante fez uma série de medições que constavam do roteiro de uma experiência. A partir destas medidas, ele fez vários cálculos para determinar os valores numéricos de algumas grandezas físicas, cujos resultados foram: 6 0 N.m , 30 kg.m/s e 20 N.m/s, correspondendo, respectivamente, às grandezas:

a) potência, força e impulso
b) energia, força e impulso
c) energia, impulso e potência
d) potência, força e energia
e) energia, potência e impulso


62. (UFPB 2004) Um garoto corre puxando um aviãozinho de plástico que se desloca a uma altura constante. A força com que o garoto puxa o aviãozinho faz um ângulo de 30º com a horizontal (ver figura abaixo). O empuxo e o atrito do ar são desprezíveis.



Nas condições descritas, pod e-se afirmar que o módulo da aceleração aplicada ao aviãozinho é:

a) 5 m/s²
b) 5/2 m/s²
c) 5/ m/s²
d) 10 m/s²
e) 10/ m/s²


63. (UFPB 2004) Dois carros de corrida percorrem, lado a lado, uma curva circular. O primeiro percorre um semicírculo de raio R1 , com velocidades angular w₁ e linear v₁ e o segundo, um semicírculo de raio R₂, com velocidades angular w₂ e linear v₂. Como os dois carros estão sempre lado a lado, os dois semicírculos são percorridos ao mesmo tempo. Sabendo-se que R₁ < R₂ , pode-se concluir que

a) w₁ = w₂ e v₁ < v₂
b) w₁ = w₂ e v₁ > v₂
c) w₁ < w₂ e v₁ < v₂
d) w₁ > w₂ e v₁ > v₂
e) w₁ = w₂ e v₁ = v₂


64. (UFPB 2004) Uma criança de 30 kg brinca de escorregar numa rampa de 2 m de altura. A criança, inicialmente em repouso, escorrega do topo da rampa e chega à base desta com uma velocidade de 4,0 m/s.
Com relação às energias envolvidas no fato descrito, pode -se dizer que

a) a energia pot encial foi transformada totalmente em energia cinética.
b) houve perda de energia mecânica devido ao atrito.
c) não houve perda de energia mecânica porque a velocidade aumentou.
d) não há atrito porque a energia mecânica se conservou.
e) a energia mecânica não se conservou porque a velocidade é maior.


65. (UFPB 2004) Uma criança de 30 kg brinca de escorregar numa rampa de 2 m de altura. A criança, inicialmente em repouso, escorrega do topo da rampa e chega à base desta com uma velocidade de 4,0 m/s.
Com base nos dados do texto, pode-se concluir que o impulso aplicado ao garoto pela força resultante foi

a) 240 kg.m/s
b) 120 kg.m/s
c) 60 kg.m/s
d) 3 0 kg.m/s
e) 1 5 kg.m/s


66. (UFPB 2004) Um estudante de física solta um bloco de madeira de massa 2 kg do ponto A da rampa, mostrada na figura abaixo. A velocidade inicial do bloco é nula. A rampa foi polida para eliminar o atrito, mas o responsável por esse trabalho esqueceu-se de polir o trecho entre os pontos B e C, que tem comprimento de 1 m. O estudante sabe que, se calcular o trabalho realizado pela força de atrito, será capaz de determinar quantas vezes o bloco passará pelo trecho BC até parar completamente.



Considerando-se que no trecho BC (e apenas nele) o coeficiente de atrito cinético entre o bloco e a rampa é m= 0,5 e que o ponto A fica a 2 m de altura, pode-se concluir que, até sua parada completa, o bloco passará, por esse trecho,

a) 1 vez
b) 2 vezes
c) 3 vezes
d) 4 vezes
e) 5 vezes


67. (UFPB 2004) Ao brincar em sua casa com carrinhos de corrida, um garoto constrói uma rampa que tem o perfil da figura abaixo.



O garoto solta uma bola de gude do ponto A, com velocidade inicial v₀ , e, à medida que a bola percorre a pista, verifica como varia sua velocidade. Desprezando-se o atrito, pode-se concluir que o gráfico que melhor representa a variação da energia cinética da bola de gude entre os pontos A e B é:

a) 
b) 
c) 
d) 
e) 


68. (UFPB 2004) Num jogo de bilhar um jogador lança a bola branc a (bola 1) com velocidade v₁ = 4 m/s em direção à bola preta (bola 2) que está parada (v₂ = 0). As bolas têm massas iguais e podem deslizar sem atrito sobre a mesa. Considerando-se que a colisão é perfeitamente elástica e frontal e que a velocidade inicial da bola branca é positiva, pode-se concluir que as velocidades das bolas, após a colisão, serão:

a) v₁ = 2 m/s e v₂ = 2 m/s
b) v₁ = – 4 m/s e v₂ = 0 m/s
c) v₁ = 0 e v₂ = 0
d) v₁ = – 4 m/s e v₂ = 4 m/s
e) v₁ = 0 e v₂ = 4 m/s


69. (UFPB ) Um garoto está brincando de soltar bolas de gude pela janela de seu apartamento. A partir de certo momento, ele resolve medir o tempo de queda dessas bolas. Seu relógio marca 10 horas 4 minutos e l segundo ao soltar uma determinada bola e ela bate, no solo, quando esse relógio marca 10 horas 4 minutos e 3 segundos. Baseado nestes dados, o garoto sabe calcular a altura de onde está soltando as bolas, ignorando a resistência do ar.
O resultado deste cálculo é:

a) 80 m
b) 45 m
c) 30 m
d) 20 m
e) 5 m


70. (UFPB 2009) Na revista Superinteressante, foi publicado um artigo afirmando que um fio de cabelo de uma pessoa cresce a uma taxa de 0,06cm ao dia. Sabendo-se que a distância entre duas camadas de átomos desse mesmo fio de cabelo é de 1,0angstrom (10^–10m) aproximadamente, é correto afirmar que o número de camadas de átomos que surgem, a cada hora, é:

a) 2,5 x 10⁵
b) 3,5 x 10⁶
c) 3,0 x 10⁶
d) 4,0 x 10⁵
e) 1,5 x 10⁴


71. (UFPB 2009) Dois homens, com auxílio de duas cordas, puxam um bloco sobre uma superfície horizontal lisa e sem atrito, conforme representação abaixo.



Considere os módulos e direções das forças exercidas pelos homens são dadas por:
• F₁ = 5 N e F₂ = 10 N
• cos θ = 0,8 e cos ø = 0,6

Nessa situação, é correto afirmar que a equação cartesiana da força resultante no bloco, em newtons, é:

a) -5i + 10j
b) 10i + 10j
c) 10i - 5j
d) -10i - 5j
e) 5i + 10j


72. (UFPB 2009) Sobre um bloco com massa 1,0kg, apoiado sobre uma mesa horizontal (figura ao lado), existe uma força dada pela equação cartesiana F = 1i + 3k, expressa no Sistema Internacional de Unidades (S.I.).



Considerando que o coeficiente de atrito cinético entre o bloco e a mesa é 0,2 e admitindo que, inicialmente, foi fornecida ao bloco uma velocidade de ao longo do eixo , é correto afirmar que o bloco, até parar, percorreu uma distância de:

a) 16 m
b) 20 m
c) 32 m
d) 40 m
e) 80 m


73. (UFPB 2009) Em uma partida de tênis, um jogador rebate uma bola com 60 gramas de massa, que chega a sua raquete com velocidade de módulo igual a 10 m/s. O impulso fornecido por esse jogador à bola tem intensidade 1,8 kgm/s, mesma direção e sentido contrário ao de incidência da bola.
Nessas circunstâncias, é correto afirmar que o módulo da velocidade da bola, logo após o rebatimento, é de:

a) 10 m/s
b) 20 m/s
c) 30 m/s
d) 40 m/s
e) 50 m/s


74. (UFPB 2009) Para analisar mudanças entre energias cinética e potencial elástica em um sistema mecânico massa-mola, um estudante de Física realiza o experimento descrito e representado abaixo:

• fixa duas molas idênticas em paredes verticais opostas;
• assinala o ponto O como o de referência e as posições das extremidades livres das molas por x₁ e -x₁;
• comprime a mola da direita com um bloco até um ponto assinalado por x₂; 
• verifica que a energia potencial do sistema é de 16J; 
• libera o bloco a partir do repouso.



A partir desse momento, o estudante observa que o bloco é arremessado em direção à mola da esquerda, que sofre uma compressão até a posição -x₂. Dessa forma, o bloco fica oscilando entre as molas.
Desprezando as perdas de energia, verifica-se que o comportamento da energia cinética do bloco, em função da sua posição, está melhor representado no gráfico:

a) 
b) 
c) 
d) 
e) 


75. (UFPB 2009) Um jogador de tênis de mesa arremessa uma bola horizontalmente, com velocidade v_o, de uma mesa com altura h. A uma distância R dessa mesa existe uma chapa metálica fina e rígida com altura h/2, conforme representado abaixo:



Nesse contexto, desprezando-se as perdas de energia da bola por atrito com o ar, ou devido a possível impacto com a chapa, identifique as afirmativas corretas:

I. O menor valor que v_o pode ter, para que a bola passe por cima da parede, é R(g/h)^1/2
II. O tempo que a bola leva para atingir o solo não depende de v_o.
III. O tempo para a bola cair a primeira metade da altura é o mesmo para a segunda metade.
IV. A componente horizontal da velocidade da bola, antes de atingir o solo, é v_o.
V. O tempo de queda da bola, em um planeta cuja aceleração da gravidade seja 2g, será maior que na Terra.


76. (UFPB 2009) Em um laboratório de Física, um estudante resolve analisar processos envolvendo colisões frontais entre corpos. Para isso prepara a experiência descrita e representada a seguir:

• sobre uma mesa lisa e sem atrito, o estudante imprime a um corpo A de massa M uma velocidade v₁;
• esse corpo choca-se, de forma perfeitamente inelástica, com o corpo B em repouso e também de massa M;
• em seguida, o conjunto (corpos A e B) colide com um terceiro corpo C, também em repouso e com massa 2M.



Nesse contexto, com relação às velocidades v₁, v₂ e v₃, representadas na figura, identifique as afirmativas corretas:

I. v₃ corresponde a 25% de v₁.
II. v₂ corresponde a 30% de v₁.
III. v₃ corresponde a 50% de v₂.
IV. v₂ corresponde a 50% de v₁.
V. v₃ é igual a v₂.


77. (UFPB 2009) No manual de instruções de uma determinada caminhonete, constam as seguintes especificações:

• Massa de 1.000kg.
• Potência máxima de 5.104W.

Considerando que, na caminhonete, atuam apenas forças conservativas, que ela parte do repouso e que foram decorridos 9 segundos do movimento desse veículo, identifique as afirmativas corretas relativas à caminhonete:

I. Não conseguirá atingir a velocidade de 40m/s.
II. Poderá atingir uma velocidade de 25m/s.
III. Poderá atingir, no máximo, uma velocidade de 27m/s.
IV. Poderá atingir, no máximo, uma velocidade de 35m/s.
V. Poderá atingir, no máximo, uma velocidade de 20m/s, quando carregada com uma carga de massa 3.000kg.



78. (UFPB 2009) Ao chegar a um posto de gasolina, um motorista vai ao calibrador e infla os pneus do seu carro, colocando uma pressão de 30bars (considere 1 bar igual a 10⁵N/m²). Nesse momento, o motorista verifica que a temperatura dos pneus é de 27⁰C. Depois de dirigir por algum tempo, a temperatura dos pneus sobe para 81⁰C. Desprezando-se o pequeno aumento no volume dos pneus e tratando o ar no seu interior como um gás ideal, é correto afirmar que, em bar, a pressão nos pneus passará a ser:

a) 35,4
b) 90,0
c) 45,5
d) 70,0
e) 54,5


79. (UFPB 2009) Em uma experiência envolvendo gases, quatro mols de um gás diatômico são aquecidos à pressão constante, a partir de uma temperatura T, fazendo com que o seu volume quadruplique. Sabendo-se que o calor molar à pressão constante do gás é (7R)/2, é correto afirmar que a energia transmitida para esse gás, em forma de calor, é:

a) 14RT
b) 42RT
c) 56RT
d) 64RT
e) 70RT


80. (UFPB 2009) Dois estudantes de Física analisam o movimento do sistema massa-mola. Eles, então, constroem uma tabela relacionando os deslocamentos sofridos pela massa em função do tempo de movimento. A representação gráfica dessa tabela é mostrada na figura abaixo.



Sabendo-se que a constante elástica da mola é de 20N/m e que a equação que relaciona o deslocamento com o tempo é dada por y=Acos(wt+π/3), é correto afirmar que a energia total do sistema massa-mola é dada por:

a) 4 x 10^-3J
b) 8 x 10^-3J
c) 16 x 10^-3J
d) 32 x 10^-3J
e) 40 x 10^-3J


81. (UFPB 2009) Em um laboratório de Física, um estudante pretende estudar o fenômeno de propagação de ondas, fazendo uso de uma corda. Uma das extremidades dessa corda foi fixada a uma parede, enquanto a outra extremidade está presa a um vibrador que produz, na corda, ondas com freqüências e velocidades desejadas (ver figura abaixo).



O estudante ajusta o vibrador para gerar ondas que se propagam com velocidade de 0,5m/s e freqüência angular w=4πrad/s. Nessas circunstâncias, adotando o Sistema Internacional de Unidades (S.I.), a função horária que melhor representa o movimento dessa onda é:

a) y=Asen[4π (2x–t)]
b) y=Asen[4π (x–2t)]
c) y=Asen[4π (x–t)]
d) y=Asen[4π (x–4t)]
e) y=Asen[4π (4x–t)]


82. (UFPB 2009) Em uma construção de um prédio de apartamentos com quatro andares, o mestre-de-obras utiliza um fio do prumo resistente, com a finalidade de verificar se uma das paredes laterais desse edifício apresenta algum tipo de defeito. Para isso, ele fixa uma das extremidades desse fio em um suporte localizado no topo do prextremidade, pendura um bloco de cimento de 6kg de massa. Dessa forma, a distância entre as duas extremidades é de, aproxi-madamente, 12 metros. A representação esquemática desse prédio, juntamente com o fio de prumo, está na figura abaixo.



Dois estudantes de Física que passavam pelo local resolvem comprovar a veracidade dos conceitos teóricos, abordados pelo professor na aula sobre ondas transversais. Para isso, eles sincronizam os seus relógios e um dos estudantes sobe até o topo do prédio, enquanto o outro fica na base, próximo ao bloco de cimento pendurado no fio. O estudante que se situa na base aplica uma pequena perturbação lateral no fio, no instante previamente determinado, a qual se propaga até o topo. O estudante que se encontra no topo observa que essa onda leva 0,5 segundos para chegar até ele. Desprezando-se a tensão no fio produzida pela sua massa e considerando g=10m/s2, é correto afirmar que a massa do fio de prumo, em quilogramas, é:

a) 1/4
b) 5/4
c) 5/2
d) 7/2
e) 9/2


83. (UFPB 2009) Uma mola considerada ideal tem uma das suas extremidades presa a uma parede vertical. Um bloco, apoiado sobre uma mesa lisa e horizontal, é preso a outra extremidade da mola (ver figura abaixo).



Nessa circunstância, esse bloco é puxado até uma distância de 6cm da posição de equilíbrio da mola. O mesmo é solto a partir do repouso no tempo t=0. Dessa forma, o bloco passa a oscilar em torno da posição de equilíbrio, x=0, com período de 2s.

Para simplificar os cálculos, considere π = 3.

Com relação a esse sistema massa-mola, identifique as afirmativas corretas:

I. O bloco tem a sua velocidade máxima de 0,18m/s na posição x=0.
II. A amplitude do movimento do bloco é de 12cm.
III. O módulo máximo da aceleração desenvolvida pelo bloco é de 0,54m/s² e ocorre nos pontos x= ± 0,06m.
IV. O bloco oscila com uma freqüência de 0,5 Hz.
V. A força restauradora responsável pelo movimento do bloco varia com o quadrado da distância do deslocamento do bloco em relação a x=0.


84. (UFPB 2009) Em um laboratório de óptica, um estudante faz incidir, sobre uma placa retangular de vidro de espessura d, um raio de luz monocromático. Sabendo que essa placa encontra-se em uma câmera de vácuo e que o ângulo formado entre o raio de luz e a normal à placa é de 30⁰, identifique as afirmativas corretas:

I. O ângulo entre o raio refletido e a normal à placa é maior do que 30⁰.
II. A velocidade da luz no interior da placa será a mesma que no vácuo.
III. O ângulo de refração do raio independe da cor da luz incidente.
IV. O ângulo que o raio de luz faz com a normal, no interior da placa, é menor do que 30⁰.
V. O raio de luz, após atravessar a placa, seguirá uma trajetória paralela à direção de incidência.


85. (UFPB 2009) Em uma feira de Ciências de sua escola, um estudante entra em um compartimento fechado que simula um submarino. Utilizando o periscópio desse “submarino”, ele observa uma colega de sua classe que está fora do compartimento. Esse periscópio compreende dois espelhos planos paralelos separados por uma distância h, inclinados 45⁰ em relação ao eixo do tubo opaco com aberturas nas extremidades (ver figura abaixo).



Considerando que a colega está a uma distância x do espelho superior, analise as afirmativas abaixo, identificando as corretas:

I. A imagem final será formada a uma distância 2x+h do espelho inferior.
II. A imagem formada no espelho superior é virtual.
III. A imagem formada no espelho inferior é real.
IV. A imagem formada no espelho inferior será direta.
V. O tamanho da imagem vista pelo estudante não depende das distâncias h e x.



86. (UFPB 2009) Dois jarros com plantas, com massas M₁ e M₂, são pendurados nas extremidades de uma haste leve e resistente de comprimento d. Essa haste é então apoiada sobre um pino vertical, também resistente, preso ao piso. A uma distância d/3 do pino está pendurado o jarro com massa M₁, conforme figura abaixo.



Nessa circunstância, para que o sistema fique em equilíbrio na posição horizontal, o valor da massa M₂ será de:

a) M₁
b) M₁/2
c) 2M₁
d) 4M₁
e) M₁/4


87. (UFPB 2009) Duas partículas de massas iguais a m estão localizadas em vértices opostos de um quadrado de lado d. Duas outras partículas, com massas iguais a 2m, estão localizadas nos outros dois vértices desse quadrado. Nessa situação, o módulo da força gravitacional que age sobre uma das partículas de maior massa é dado por:

a) Gm²/d²(1 + 2)
b) 3Gm²/d²
c) Gm²/d²
d) 2Gm²/d²
e) (3/2)Gm²/d²


88. (UFPB 2009) Deseja-se utilizar uma ventosa, objeto similar a um desentupidor de uso doméstico, para pendurar um jarro com plantas ornamentais em uma sala, situada em uma casa ao nível do mar, cujo teto é bastante liso e resistente. Para realizar essa tarefa, considere as seguintes informações:

• a massa do jarro com a planta é de, aproximadamente, 10 kg;
• a ventosa tem massa desprezível e é esvaziada completamente (caso ideal).

Nesse contexto, para que a ventosa possa segurar esse jarro, a área mínima necessária dessa ventosa é de:

a) 1,0 cm²
b) 5,0 cm²
c) 10,0 cm²
d) 15,0 cm²
e) 20,0 cm²


89. (UFPB 2009) Uma bateria de força eletromotriz 14 V e resistência interna 2Ω é conectada a um resistor com resistência igual a 5Ω, formando um circuito elétrico de uma única malha, conforme representação abaixo.



Nesse contexto, quando o voltímetro é ligado aos pontos A e B do circuito, a leitura correta desse voltímetro é:

a) 10 V
b) 15 V
c) 20 V
d) 25 V
e) 30 V


90. (UFPB 2009) Em uma espira retangular condutora, conforme figura ao lado, circula uma corrente i no sentido horário.



Nesse caso, a expressão para o campo magnético total no centro da espira é:

a) B = 6 μ_oi/(πL), entrando na página.
b) B = 8 μ_oi/(πL), saindo do plano da página.
c) B = 0.
d) B = 6 μ_oi/(πL), saindo do plano da página.
e) B = 8 μ_oi/(πL), entrando no plano da página.


91. (UFPB 2009) Dois capacitores, com capacitâncias C₁ = 8 μF e C₂ = 4 μF, são carregados separadamente, quando submetidos a uma mesma diferença de potencial ΔV_i fornecida por uma bateria. Os capacitores são desconectados da bateria e suas placas são, em seguida, reconectadas, porém com polaridades invertidas, conforme figura abaixo.



Nesse contexto, a diferença de potencial, ΔV_f, à qual ficam submetidos esses capacitores quando as chaves são fechadas, está corretamente expressa, em termos de VΔi, por:

a) ΔV_f = 1/3ΔV_i
b) ΔV_f = ΔV_i
c) ΔV_f = 3ΔV_i
d) ΔV_f = 2/3ΔV_i
e) ΔV_f = 1/2ΔV_i


92. (UFPB 2009) Em uma aula sobre Gravitação, um professor de Física propõe aos seus alunos analisarem o sistema constituído por um planeta de massa m e raio r, o qual se encontra em órbita circular de raio R₀ em torno de uma estrela de raio R e massa M. Com o objetivo de avaliar os conhecimentos desses alunos acerca do assunto, o professor elabora as afirmativas abaixo. Considerando R₀ >> R + r, dentre essas afirmativas, identifique as corretas:

I. Se a massa do planeta fosse 2m, o período de rotação não se alteraria.
II. Se o raio do planeta fosse 2r, o período de rotação não se alteraria.
III. Se o raio da órbita fosse 2R₀, o período de rotação não se alteraria.
IV. Se o raio da estrela fosse 2R, o período de rotação não se alteraria.
V. Se a massa da estrela fosse 2M, o período de rotação não se alteraria.


93. (UFPB 2009) Em um laboratório de Física, dois estudantes pretendem estudar possíveis dependências da altura da coluna de mercúrio com a pressão atmosférica e as formas dos vasos que contêm essa substância. Para isso, eles usam um tubo de ensaio com raio R, enchendo-o completamente com mercúrio. Em seguida, colocam esse tubo em posição invertida em um recipiente, que também contém mercúrio. O tubo então é destampado, e observa-se que a altura da coluna de mercúrio no tubo é h, conforme representação na figura 1.



Nesse contexto, identifique as afirmativas corretas:

I. A altura da coluna de mercúrio será menor do que h, se essa mesma experiência for realizada no topo de uma montanha muito alta.
II. A altura da coluna de mercúrio será menor do que h, se essa mesma experiência for repetida usando um tubo com raio 2R.
III. A altura da coluna de mercúrio será maior do que h, se o recipiente da figura 1 for trocado pelo da figura 2.
IV. A altura da coluna de mercúrio será maior do que h, se o recipiente da figura 1 for trocado pelo da figura 3.
V. A altura da coluna será maior do que h, se o mercúrio for substituído por água.


94. (UFPB 2009) Sobre energia potencial elétrica e potencial elétrico, identifique as afirmativas corretas:

I. Ao se deslocar um objeto carregado entre dois pontos, em uma região do espaço onde existe um campo elétrico, a diferença de potencial medida entre esses dois pontos independe da carga do objeto.
II. A variação da energia potencial elétrica associada a um objeto carregado, ao ser deslocado de um ponto para outro em uma região onde exista um campo elétrico, independe da trajetória seguida entre esses dois pontos.
III. A energia potencial elétrica é uma grandeza associada a um sistema constituído de objetos carregados e é medida em volts (V).
IV. Um elétron-volt, 1eV, é a energia igual ao trabalho necessário para se deslocar uma única carga elementar, tal como elétron ou próton, através de uma diferença de potencial exatamente igual a 1 (um) volt. E a relação dessa unidade com Joule (J) é, aproximadamente, 1 eV = 1,6 x 10^-19J.
V. A energia potencial elétrica, associada a uma carga teste, q_o, positiva, aumenta quando esta se move no mesmo sentido do campo elétrico.


95. (UFPB 2009) Em um laboratório de eletricidade e magnetismo, um grupo de estudantes analisa os efeitos produzidos pelo movimento relativo entre um ímã e uma espira condutora, conforme representação na figura abaixo.



Considerando essas informações, identifique as afirmativas que descrevem corretamente os fenômenos a serem observados pelos estudantes:

I. Ao se fixar a espira e dela ser aproximado o ímã, uma corrente induzida na espira com sentido horário é observada.
II. Ao se fixar o ímã e dele ser afastada a espira, uma corrente induzida na espira com sentido horário será observada.
III. Ao se fixar a espira e dela ser afastado o ímã, uma corrente induzida na espira no sentido horário é observada.
IV. Ao se fixar o ímã e dele ser aproximada a espira, uma corrente induzida no sentido anti-horário será observada.
V. Para induzir uma corrente na espira, é suficiente que um fluxo de linhas de indução de campo magnético atravesse essa espira.


Respostas 1. a    2. d    3. b    4. e    5. d    6. c    7. c    8. e    9. b    10. d    11. c    12. e    13. a    14. b    15. e    16. d    17. d    18. c    19. b    20. a    21. e    22. d    23. e    24. b    25. c    26. c    27. a    28. e    29. c    30. a    31. d    32. e    33. e    34. d    35. b    36. d    37. e    38.a    39. 10    40. 18    41. 28    42. 40    43. 16    44. 20    45. d    46. e    47. d    48. a    49. c    50. b    51. a    52. c    53. c    54. d    55. a    56. c    57. b    58. d    59. a    60. e    61. c    62. d    63. a    64. b    65. b    66. d    67. a    68. e    69. d    70. a    71. c    72. b    73. b    74.a    75. I, II e IV    76. I, III e IV    77. I e II    78. a    79. b    80. c    81. a    82. b    83. I, III e IV    84. IV e V    85. III, IV e V    86. b    87. b    88.b    89. a    90. a    91. a    92. I, II e IV    93. I e V    94. I, II e IV    95. II, III e IV





Fonte: 

http://www.fisicapaidegua.com/prova.php?fonte=UFPB&amp;ano=2007

https://www.sofisica.com.br/conteudos/Mecanica/Cinematica/questoes.php