Movimento Retilíneo Uniformemente Variado Exercícios Resolvidos Cálculos
1. Testes realizados com o carro Gol mostraram que ele vai de 0 a 100 km/h em 10s. Calcule a aceleração aproximada do veículo nesse intervalo de tempo. (adote 100 km/h = 28 m/s)
a) 2,0 m/s²
b) 2,8 m/s²
c) 4,1 m/s²
d) 5,3 m/s²
e) 8,1 m/s²
Resolução
v0 = 0
v = 100 km/h = 28 m/s
t = 10 s
v = v0 + a.t
28 = 0 + a . 10
10a = 28
a = 28/10
a = 2,8 m/s²
2. Um automóvel que vinha a 25 m/s freou e parou em 25 s. O valor da aceleração escalar média do automóvel durante a freada foi de:
a) zero
b) -1,0 m/s²
c) 1,0 m/s²
d) -3,6 m/s²
e) 4,0 m/s²
Resolução
v0 = 25 m/s
v = 0
t = 25 s
v = v0 + a.t
0 = 25 + a . 25
25 + a . 25 = 0
25 + a . 25 = 0
25a = -25
a = -25/25
a = -1 m/s²
3. Um avião a jato, partindo do repouso. é submetido a uma aceleração constante de 4 m/s². Qual o intervalo de tempo de aplicação desta aceleração para que o jato atinja a velocidade de decolagem de 160 m/s ?
a) 80s
b) 20s
c) 20s
d) 40s
e) 40s
Resolução
v0 = 0
v = 160 m/s
a = 4 m/s²
v = v0 + a.t
160 = 0 + 4.t
t = 160/4
t = 40 s
4. A equação da velocidade de um móvel em movimento retilíneo é dada por v= 50 -4t, no sistema internacional. A velocidade desse móvel no instante 5 segundos é:
a) 50 m/s
b) 40 m/s
c) 30 m/s
d) 60 m/s
e) 70 m/s
Resolução
t = 5 s
v = 50 - 4.t
v = 50 - 4 . 5
v = 50 - 20
v = 30 m/s
|
EXERCÍCIOS MUV
1. Durante uma corrida de carros, um dos competidores consegue atingir 100km/h desde a largada em 5s. Qual a aceleração média por ele descrita?
2. Um móvel, partindo do repouso com uma aceleração constante igual 1m/s² se desloca durante 5 minutos. Ao final deste tempo, qual é a velocidade por ele adquirida?
3. Um automóvel encontra-se parado diante de um semáforo. Logo quando o sinal abre, ele arranca com aceleração 5m/s², enquanto isso, um caminhão passa por ele com velocidade constante igual a 10m/s.
(a) Depois de quanto tempo o carro alcança o caminhão?
(b) Qual a distância percorrida até o encontro.
Escreve-se as equações do muv para o carro e do mu para o caminhão:
Carro:
Caminhão:
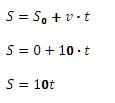
Quando os dois se encontram, suas posições são iguais, então:
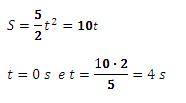
(b) Sabendo o momento do encontro, só é necessário aplicá-lo em uma das duas funções (do caminhão ou do carro).
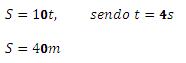
Logo o carro encontra o caminhão 4 segundos após a sinaleira abrir, a uma distância de 40 m.
4. Uma motocicleta se desloca com velocidade constante igual a 30m/s. Quando o motociclista vê uma pessoa atravessar a rua freia a moto até parar. Sabendo que a aceleração máxima para frear a moto tem valor absoluto igual a 8m/s², e que a pessoa se encontra 50m distante da motocicleta. O motociclista conseguirá frear totalmente a motocicleta antes de alcançar a pessoa?
Como a aceleração utilizada para frear a moto se opõe ao movimento, tem valor negativo, então:
A motocicleta não irá parar antes de atingir a pessoa.
5. Um corredor chega a linha de chegada em uma corrida com velocidade igual a 18m/s. Após a chegada ele anda mais 6 metros até parar completamente. Qual o valor de sua aceleração?
Movimento Vertical
1. Uma pedra é abandonada de um penhasco de 100m de altura. Com que velocidade ela chega ao solo? Quanto tempo demora para chegar?
2. Em uma brincadeira chamada "Stop" o jogador deve lançar a bola verticalmente para cima e gritar o nome de alguma pessoa que esteja na brincadeira. Quando a bola retornar ao chão, o jogador chamado deve segurar a bola e gritar: "Stop", e todos os outros devem parar, assim a pessoa chamada deve "caçar" os outros jogadores. Quando uma das crianças lança a bola para cima, esta chega a uma altura de 15 metros. E retorna ao chão em 6 segundos. Qual a velocidade inicial do lançamento?
Para realizar este cálculo deve-se dividir o movimento em subida e descida, mas sabemos que o tempo gasto para a bola retornar é o dobro do tempo que ele gasta para subir ou descer. Então:
- Subida (t=3s)
3. Durante a gravação de um filme, um dublê deve cair de um penhasco de 30m de altura e cair sobre um colchão. Quando ele chega ao colchão, este sofre uma deformação de 1m. Qual é a desaceleração que o dublê sofre até parar quando chega colchão?
A desaceleração sofrida pelo dublê se dará quando a velocidade inicial for a velocidade de chegada ao solo na queda vertical, a velocidade final for zero, e a distância do deslocamento for 1m de deformação do colchão. Então o primeiro passo para chegar a resolução é descobrir a velocidade de chegada ao solo:
Como no exercício não é dado o tempo, a maneira mais rápida de se calcular a velocidade é através da Equação de Torricelli para o movimento vertical, com aceleração da gravidade positiva, já que o movimento é no mesmo sentido da gravidade.
O segundo passo é calcular o movimento uniformemente variado para a desaceleração da queda. Com velocidade inicial igual a 24,5m/s.
4. Um fazendeiro precisa saber a profundidade de um poço em suas terras. Então, ele abandona uma pedra na boca do poço e cronometra o tempo que leva para ouvir o som da pedra no fundo. Ele observa que o tempo cronometrado é 5 segundos. Qual a altura do poço?
Podemos dividir o movimento em movimento da pedra e o deslocamento do som.
- Movimento da Pedra:
- Deslocamento do som:
Sabendo que a altura do poço é a mesma para as duas funções e que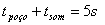 
:
:
mas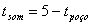 
, então:
, então:
Sabendo que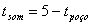
Tendo os tempos de cada movimento, podemos calcular a altura utilizando qualquer uma das duas funções:
MAIS EXERCÍCIOS
01. Qual o conceito físico de aceleração?
02. O que se pode afirmar sobre a aceleração, num movimento uniformemente variado?
03. Qual a diferença entre um movimento variado e um movimento uniformemente variado?
04. Qual a função horária das velocidades em um M.U.V.?
05. Qual a função horária dos espaços em um M.U.V.?
06. Qual é a equação de TORRICELLI?
07. Quando um movimento pode ser dito ACELERADO? E RETARDADO?
08. Preencha o quadro abaixo, utilizando sinais (+) ou (-) para a velocidade e para a aceleração, conforme o tipo de movimento.
TIPO DE MOVIMENTO
|
v
|
a
|
Progressivo e retardado
| ||
Retrógrado e retardado
| ||
Retrógrado e acelerado
| ||
Progressivo e acelerado
|
09. Complete a tabela abaixo, no SIU
S = f(t)
|
v = f(t)
|
So
|
vo
|
a
|
S = 4 - 3.t + 4.t2
| ||||
S = 4.t - 3.t2
| ||||
S = 8 - 5.t2
| ||||
S = t.2
| ||||
S = 3,2t2 -1,4t + 5
| ||||
v = 5.t - 1
|
3
| |||
v = -6.t
|
-9
| |||
3
|
0
|
-6
| ||
0
|
0
|
-2
| ||
4
|
-1
|
10
|
10. Para cada uma das funções da tabela acima, pede-se determinar:
a) a posição do móvel no 3o segundo
b) a velocidade do móvel no 3o segundo
c) o instante em que o móvel inverte o sentido do movimento
d) o(s) instante(s) em que o móvel passa pela origem da trajetória
e) o deslocamento escalar do móvel do 1o ao 5o segundos
f) o gráfico de aceleração em função do tempo
g) o gráfico de velocidade em função do tempo
h) o gráfico de espaço em função do tempo.
11. Num movimento, a velocidade escalar do móvel varia em função do tempo, de acordo com os valores apresentados na tabela a seguir. O sinal da velocidade indica o sentido do movimento segundo uma orientação da trajetória.
t(s)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
v(m/s)
|
10
|
8
|
6
|
4
|
2
|
0
|
-2
|
-4
|
-6
|
Determine:
a) se o movimento é uniforme ou variado (justifique)
b) a velocidade inicial do móvel
c) se o movimento é acelerado ou retardado nos intervalos de 0s a 4 s e de 6s a 8s
d) a aceleração escalar média de 0s a 2s, de 3s a 5s, de 4s a 7s
12. Um ponto material está animado de MUV com aceleração igual a - 2m/s2. Sua velocidade escalar varia com o tempo, segundo os dados da tabela anexa. Determine:
a) a velocidade escalar inicial do movimento
b) em que intervalos de tempo o movimento é acelerado, em que intervalos de tempo é retardado
c) em que intervalos de tempo o movimento é progressivo, em que intervalos de tempo é retrógrado.
t(s)
|
0
|
1
|
2
|
3
|
4
|
5
|
v(m/s)
|
6
|
4
|
2
|
0
|
-2
|
-4
|
13. É dada a função v = 12 - 2.t, onde t é medido em segundos e v é medido em m/s.
a) Determine a velocidade escalar inicial e a aceleração escalar do movimento
b) discuta se o movimento é acelerado ou retardado nos instantes 2s e 8s
c) verifique se há mudança no sentido do movimento (se houver, em que instante)
14. É dado o movimento cujo espaço S, medido na trajetória (em metros) a partir de uma origem, varia em função do tempo conforme:
S = 10 - 2.t + t2/2
onde os instantes t são medidos em segundos.
a) Determine o tipo do movimento (uniforme ou uniformemente variado)
b) Determine o espaço e a velocidade iniciais e a aceleração escalar
c) Determine a função da velocidade
d) Verifique se o móvel muda de sentido de movimento; se mudar, determine o espaço nesse instante.
15. Um móvel descreve um MUV numa trajetória retilínea e os seus espaços variam com o tempo de acordo com a função horária, no SIU
S = 9 + 3.t - 2.t2
Determine:
a) a função da velocidade escalar
b) o instante em que o móvel passa pela origem dos espaços
16. Um ponto material parte do repouso com movimento uniformemente variado (acelerado), de aceleração escalar a = 5 m/s2. Qual sua velocidade e seu espaço após 10 s?
17. Sobre uma mesma trajetória, dois moveis A e B se movimentam obedecendo às funções horárias:
SA = - 10 + 20.t e SB = 15 + 5.t + 2.t2 (S em metros e t em segundos). Determine:
a) em que instantes os moveis A e B se cruzam?
b) onde, na trajetória, ocorrem os cruzamentos dos moveis?
18. Um automóvel está parado diante de um sinal fechado. No instante em que o farol fica verde, passa por ele uma motocicleta que mantém constante uma velocidade de 15 m/s. Supondo que, nesse mesmo instante, o automóvel comece a se mover com aceleração constante igual a 2 m/s2, determine:
a) após quanto tempo o automóvel alcança a moto;
b) que distância o automóvel percorre até alcançar a moto;
c) a velocidade do automóvel no instante em que alcança a moto.
19. Ao ver passar uma bela garota loura dirigindo uma Ferrari vermelha que desenvolve velocidade constante de 72 km/h, um apaixonado rapaz resolve sair ao seu encalço pilotando sua possante moto. No entanto, ao conseguir partir com a moto, com aceleração constante igual a 4 m/s2, o carro já está 22 m à frente.
a) Após quanto tempo o rapaz alcança o carro da moça?
b) Que distância a moto percorreu até o instante em que os dois veículos se emparelham?
c) Qual a velocidade da moto no instante em que alcança o carro?
20. Um carro a 90 Km/h é freado uniformemente com a aceleração escalar de 2,5 m/s2 (em módulo) até parar. Determine a variação do espaço do móvel desde o início da freagem até parar.
21. Um móvel parte do repouso e com aceleração constante de 5 m/s2, atinge a velocidade de 20 m/s. Determine a variação de espaço do móvel enquanto sua velocidade variava.
22. A velocidade escalar de um trem se reduz uniformemente de 12 m/s para 6 m/s. Sabendo-se que durante esse tempo o trem percorre a distância de 100 m, qual o módulo de sua desaceleração?
23. Um composição do metrô parte de uma estação, onde estava em repouso, e percorre 100 m com aceleração escalar constante atingindo 20 m/s. Determine a aceleração escalar e a duração do processo.
24. Uma locomotiva parte do repouso de uma estação e percorre 100 m com aceleração constante. Depois de quanto tempo e com que valor de aceleração a locomotiva atinge a velocidade de 72 km/h?
25. Um trem de metrô parte de uma estação com aceleração constante, até atingir, após 10 s, a velocidade de 90 km/h, que é mantida durante 30 s, para então desacelerar uniformemente durante 10 s até parar na estação seguinte.
a) Represente graficamente a velocidade em função do tempo.
b) Calcule a distância entre as duas estações.
26. Um ponto material percorre uma distância de 60 m em 6 s, com aceleração constante. Se sua velocidade final é de 15 m/s, pede-se:
a) Qual sua aceleração?
b) Qual sua velocidade inicial?
27. Um trem de 120m de comprimento se desloca com velocidade escalar de 20 m/s. Esse trem, ao iniciar a travessia de uma ponte, freia uniformemente, saindo completamente da mesma 10 s após, com velocidade escalar de 10 m/s. Qual o comprimento da ponte?
28. Uma partícula parte do repouso, no instante inicial, com aceleração constante e percorre 18 m nos primeiros 3 segundos. Aos 4 s de movimento uniformemente variado, qual será a velocidade da partícula?
29. Um trem deve partir de uma estação A e parar na estação B, distante 4000 m de A. A aceleração e a desaceleração podem ser, no máximo, de 5 m/s2, e a maior velocidade que o trem atinge é de 20 m/s. Qual o tempo mínimo para o trem completar o percurso de A a B?
30. Um corpo tem, num ponto A de sua trajetória retilínea, a velocidade de 36 km/h e, em um ponto B, a 100 m de A, a velocidade de 54 km/h. O movimento é uniformemente variado.
a) Qual o tempo gasto em percorrer a distância AB?
b) A que distância se encontrará de A decorridos 10 s da passagem por B?
c) Qual sua velocidade nesse instante?
31. Um carro parte do repouso de um ponto A com uma aceleração constante em módulo igual a 10 m/s2. Quando sua velocidade atinge o valor de 20 km/h passa a se mover com movimento uniforme durante um intervalo de tempo igual a 15 minutos. No fim desse tempo aplicam-se os freios constantemente e o carro pára num ponto B, distante 15 m do ponto onde foi iniciado o movimento retardado. Determine a distância entre os pontos A e B.
32. A velocidade de um carro é, no instante em que o motorista nota que o sinal fechou, 72 km/h. O tempo de reação do motorista é de 0,7 s (tempo de reação, tempo decorrido entre o instante em que o motorista vê o sinal fechar até aquele em que aplica os freios) e os freios aplicam ao carro um retardamento uniforme de 5 m/s2. Qual a distância percorrida pelo carro, do instante em que o motorista nota que o sinal fechou até parar.
33. Dois moveis partem do repouso, de um mesmo ponto, no mesmo instante t = 0, percorrendo uma trajetória retilínea, com acelerações constantes. Sabe-se que a aceleração de um dos moveis é o dobro da do outro. No instante t = 10 s, a distância entre os moveis é 600 m. Calculara a aceleração dos moveis.
34. Um móvel parte do repouso da origem das posições de uma trajetória retilínea com aceleração constante de 2 m/s2. Após 20 s, começa a frear uniformemente até parar a 500 m do ponto de partida. Calcule o módulo da aceleração de freagem do móvel.
35. Um carro parte do repouso, de um ponto A, movendo-se com aceleração constante sobre uma trajetória retilínea. Sabendo que esse carro passa por um ponto B com velocidade de 12 m/s e pelo ponto C distante 45 m de B, com velocidade de 18 m/s, calcule:
a) a aceleração do carro;
b) o tempo gasto para passar por B e por C;
c) o tempo gasto para percorrer a distância BC;
d) as distâncias AB e AC
GABARITO
01.Medida da rapidez de mudança de velocidade
02. É constante
03. Mov. variado - aceleração variável
Mov. Un. Variado - aceleração constante
04. v = vo + a.t
05. S = So + vo.t + a/2.t2
06. v2 = vo2 + 2.a.∆S
07. Acelerado=v e a com sinais iguais
Retardado = v e a com sinais constrários
08.
+
|
-
|
-
|
+
|
-
|
-
|
+
|
+
|
09.
S = f(t)
|
v = f(t)
|
So
|
vo
|
a
|
v = -3 + 8.t
|
4
|
-3
|
8
| |
v = 4 - 6.t
|
0
|
4
|
-6
| |
v = -10.t
|
8
|
0
|
-10
| |
v = 2.t
|
0
|
0
|
2
| |
v = - 1,4 + 6,4.t
|
5
|
-1,4
|
6,4
| |
S = 3 - t + 2,5.t2
|
-1
|
5
| ||
S = - 9 - 3.t2
|
0
|
-6
| ||
S = 3 - 3.t2
|
v = -6.t
|
0
|
-6
| |
S = - t2
|
v = - 2.t
| |||
S = 4 - t + 5.t2
|
v = -1 + 10.t
|
10.
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII
|
IX
|
X
| |
a
|
31
|
- 15
|
- 37
|
9
|
29,6
|
22,5
|
- 36
|
- 24
|
-9
|
46
|
b
|
21
|
- 14
|
- 30
|
6
|
17,8
|
14
|
- 18
|
- 18
|
- 6
|
29
|
c
|
0,375
|
0,667
|
0
|
0
|
0,219
|
0,2
|
0
|
0
|
0
|
0,1
|
d
|
nunca
|
1,3 e0
|
1,26
|
0
|
nunca
|
nunca
|
nunca
|
1
|
0
|
nunca
|
e
|
84
|
- 56
|
-128
|
24
|
66,2
|
53
|
- 63
|
- 75
|
-24
|
112
|
11. a) M.U.V pois v varia de 2m/s a cada segundo
b) vo = 10 m/s
c) 0 a 4 s = retardado
6 s a 8 s = acelerado
d) a0-2 = a3-5 = a 4-7 = - 2 m/s2
12. a) vo = 6 m/s
b) 0 a 3 s = retardado
após 3 s = acelerado
c) de 0s a 3 s = progressivo
após 3 s = retrógrado
13. a) vo = 12 m/s e a = - 2 m/s2
b) retardado
acelerado
c) 6 s
14. a) M.U.V.
b) 10 m, - 2 m/s, 1 m/s2
c) v = - 2 + t
d) 2 s e 8 m
15. a) v = 3 - 4.t
b) 3 s
16. 50 m/s e 250 m
17. 5 s e 90 m
18. a) 15 s
b) 225 m
c) 30 m/s
19. a) 11 s
b) 242 m
c) 44 m/s
20. 125 m
21. 40 m
22. - 0,54 m/s2
23. 2 m/s2
24. 10 s e 2 m/s2
25. a) gráfico
b) 1000 m
26. a) 5/3 m/s2
b) 5 m/s
27. 30 m
28. 16 m/s
29. 204 s
30. a) 8 s
b) 281,25 m
31. 5020,55 m
32. 54 m
33. 12 m/s2 e 24 m/s2
34. - 8 m/s2
35. a) 2m/s2
b) 6 s e 9 s
c) 3 s
d) 36 m e 81 m
Comentários