PA Exercícios Resolvidos
A cada aniversário, seu bolo tem uma quantidade de velas igual à sua idade. As velas são vendidas em pacotes com 12 unidades e todo ano é comprado apenas um novo pacote. As velas remanescentes são guardadas para os anos seguintes, desde o seu primeiro aniversário.
Qual a sua idade, em anos, no primeiro ano em que as velas serão insuficientes?
a) 12.
b) 23.
c) 24.
d) 36.
e) 38.
» Resposta:
(AFA 2017) - QUESTÃO
Constrói-se um monumento em formato de pirâmide utilizando-se blocos cúbicos:
Para a formação piramidal os blocos são dispostos em uma sequência de camadas, sendo que na última camada, no topo da pirâmide, haverá um único bloco como mostra a figura a seguir.

A disposição total, foram utilizados 378 blocos, do topo à base da pirâmide. Havendo necessidade de acrescentar uma nova camada de blocos abaixo da base da pirâmide, obedecendo à sequência já estabelecida, serão gastos x blocos nesta camada.
A quantidade total de divisões positivos do número x é igual a:
a) 2.
b) 3.
c) 4.
d) 5.
» Resposta:
(IME 2017) - QUESTÃO
Sejam uma progressão aritmética (a1, a2, a3, a4, ...) e uma progressão geométrica (b1, b2, b3, b4, …) de termos inteiros, de razão r e razão q, respectivamente, onde r e q são inteiros positivos, com q > 2 e b1 > 0. Sabe-se, também, que a1+b2 = 3, a4+b3=26. O valor de b1 é:
a) 1
b) 2
c) 3
d) 4
e) 5
» Resposta:
QUESTÃO - (ESA 2008)
Quantos múltiplos de 9 ou 15 há entre 100 e 1000?
a) 100
b) 120
c) 140
d) 160
e) 180
» Resposta:
QUESTÃO - ( EEAR 2013)
As medidas dos ângulos internos de um triângulo formam uma PA. Assim, independente do valor da razão, pode-se afirmar que um desses ângulos mede:
a) 30◦
b) 45◦
c) 60◦
d) 90◦ .
________________
RESPOSTA: C
» Resposta:
QUESTÃO
(UERN) A sequência de números positivos (x, x + 10, x², ...) é uma progressão aritmética, cujo décimo termo é:
A) 94
B) 95
C) 101
D) 104
E) 105
RESPOSTA: B
QUESTÃO
(PUC-SP) O número de múltiplos de 7 entre 1.000 e 10.000 é:
a) 1280
b) 1284
c) 1282
d) 1286
e) 1288
RESPOSTA: D
QUESTÃO
(MACK-SP) Numa progressão aritmética de 100 termos, a3 = 10 e a98 = 90, a soma de todos os termos é:
a) 10.000
b) 9.000
c) 4.500
d) 5.000
e) 7.500
RESPOSTA: D
QUESTÃO
(PUC-RIO) Temos uma progressão aritmética de 20 termos onde o 1º termo é igual a 5. A soma de todos os termos dessa progressão aritmética é 480. O décimo termo é igual a:
A) 20
B) 21
C) 22
D) 23
E) 24
RESPOSTA: D
QUESTÃO
(PUC-RIO) A soma de todos os números naturais ímpares de 3 algarismos é:
A) 220.000
B) 247.500
C) 277.500
D) 450.000
E) 495.000
RESPOSTA: B
QUESTÃO
(PUC-RIO) Numa progressão aritmética de razão r e primeiro termo 3, a soma dos primeiros n termos é 3n², logo, a razão é:
A) 2
B) 3
C) 6
D) 7
E) 9
RESPOSTA: C
QUESTÃO
(UDESC) A soma dos quatro primeiros termos de uma progressão geométrica (PG) de razão 3 é igual a 60, e a soma dos quatro primeiros termos de uma progressão aritmética (PA) também vale 60. Sabe-se que o primeiro termo da PA é igual ao primeiro termo da PG. A razão da PA é:
A) -3
B) 3/2
C) 3
D) 2/3
E) 9
RESPOSTA: E
(ADVISE) Seja (a, b, c) uma progressão aritmética de razão real e de termos não nulos. Sendo assim podemos sempre afirmar que:
A) a + b = b + c
B) b = a + c
C) b² = ac
D) a – 2b + c = 0
E) 2c = a + b
RESPOSTA: D
QUESTÃO
Qual o primeiro termo de uma PG com 8 termos, onde o último vale -1 e a razão 1/2 ?
A) – 128
B) 128
C) – 156
D) 156
E) 200
RESPOSTA: A
QUESTÃO
Uma P.G é formada por 6 termos, onde a1 = 4 e a6 = 972. A soma dos elementos que formam os meios geométricos existentes entre a1 e a6 vale:
A) 320
B) 324
C) 40
D) 450
E) 480
RESPOSTA: E
QUESTÃO
(ESA) Em um treinamento de condicionamento físico, um soldado inicia seu primeiro dia correndo 800 m. No dia seguinte corre 850 m. No terceiro 900 m e assim sucessivamente até atingir a meta diária de 2.200 m. Ao final de quantos dias, ele terá alcançado a meta?A) 31
B) 29
C) 27
D) 25
E) 23
RESPOSTA: B
QUESTÃO
(Unifor-CE) As distâncias que seis trabalhadores percorrem diariamente para ir de suas casas à fábrica onde trabalham são numericamente iguais aos termos de uma PA. Se a casa mais próxima da fábrica fica a 1 km dela e a mais distante, a 8,5 km, a soma das distâncias que os seis percorrem diariamente para ir de suas casas até a fábrica, em quilômetros, é igual a:
A) 20
B) 22,5
C) 25
D) 28,5
E) 30
RESPOSTA: D
QUESTÃO
(MACK-SP) A caixa d’água reserva de um edifício, que tem capacidade para 25 000 litros, contém, em determinado dia, 9 600 litros. Contrata-se uma empresa para fornecer 400 litros de água nesse dia, 600 litros no dia seguinte, 800 litros no próximo, e assim por diante, aumentando em 200 litros o fornecimento de cada dia. O número de dias necessários para que a caixa atinja a sua capacidade total é:
A) 11
B) 13
C) 14
D) 12
E) 10
RESPOSTA: A
QUESTÃO
(UFMT) Em uma clínica ortodôntica são atendidos 30 clientes diários de segunda a sexta-feira. Para redimensionar a estrutura física, a clínica passará a atender da seguinte maneira: dois clientes no primeiro dia do mês, quatro no segundo, seis no terceiro, oito no quarto e assim sucessivamente. Considerando que essa clínica atende 20 dias por mês, o número de clientes atendidos, em um mês, será reduzido em:
A) 35%
B) 30%
C) 40%
D) 25%
E) 70%
RESPOSTA: B
QUESTÃO
(ADVISE) Seja (a, b, c) uma progressão aritmética de razão real e de termos não nulos. Sendo assim podemos sempre afirmar que:
A) a + b = b + c
B) b = a + c
C) b² = ac
D) a – 2b + c = 0
E) 2c = a + b
GABARITO: D
FONTE: http://projeto-militar.blogspot.com/search/label/Progress%C3%A3o%20Aritm%C3%A9tica%20%28PA%29
Exercício 01 – (UFRGS) Em uma Progressão Aritmética, em que o primeiro termo é 23 e a razão é -6, a posição ocupada pelo elemento -13 é:
a) 8ª
b) 7ª
c) 6ª
d) 5ª
e) 4ª
Esse exercício é pura aplicação da fórmula do termo geral da PA. O enunciado nos forneceu todos os elementos da fórmula, exceto o número de termos. Vamos substituir na fórmula os dados do exercício e isolar n.

Exercício 2 – (UCS) O valor de x para que a sequência (2x, x+1, 3x) seja uma PA é:
a) 1/2
b) 2/3
c) 3
d) 1/2
e) 2
Sabemos que a razão da PA é uma constante, portanto vamos igualar a razão calculando ela de duas formas: 2º termo menos o 1º termo e o 3º termo menos o 2º termo. Feito isso, basta isolar x.
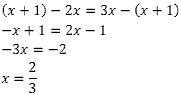
Exercício 3 – (FUVEST) Em uma progressão aritmética de termos positivos, os três primeiros termos são 1 – a, -a, . O 4° termo é:
a) 2
b) 3
c) 4
d) 5
e) 6
Vamos iniciar o exercício calculando a razão. Vamos pegar o 2º termo e subtrair o 1º termo.

Feito isso, vamos calcular o 3º termo somando o segundo termo mais a razão. Encontrando o 3º termo, vamos iguala-lo ao 3º termo informado pelo exercício e vamos elevar os dois ao quadrado para sumirmos com a raiz quadrada.

Você pode resolver a equação do 2º grau de diversas formas, mas aqui eu escolhi resolver por soma e produto.
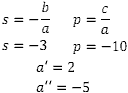
Para saber qual é a resposta certa, devemos verificar qual delas atende às duas restrições geradas por conta da raiz quadrada. Por se tratar de termos positivos, o número dentro da raiz quadrada não pode ser negativo senão torna-se número complexo. Qualquer que seja o número dentro da raiz quadrada, o resultado deve ser maior ou igual a zero. Com isso, temos essas duas restrições:

Vamos testar a=2.
11-2=9 e -2-1=-3. Observem que o segundo resultado foi menor do que zero, portanto não satisfaz a restrição. Descartamos 2 como resposta.
Vamos testar a=-5.
11-5=6 e –(-5)-1=4. As duas restrições foram satisfeitas, portanto a=-5.
Agora temos a razão e o valor de a. Nem é preciso aplicar fórmula:
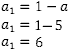
Portanto: PA(6,5,4,3…)
Letra b.
Se você não conseguiu resolver esse exercício, não desanime, pois ele é considerado difícil.
Exercício 4 – (PUC-RIO 2009) Temos uma progressão aritmética de 20 termos onde o 1º termo é igual a 5. A soma de todos os termos dessa progressão aritmética é 480. O décimo termo é igual a:
a) 20
b) 21
c) 22
d) 23
e) 24
Os dados fornecidos pelo exercício são:
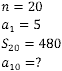
Vamos iniciar calculando o vigésimo termo da PA.

Vamos calcular a razão da PA.
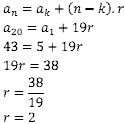
Agora vamos calcular o décimo termo da PA.
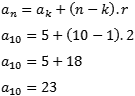
Exercício 5 – (UDESC 2008) A soma dos quatro primeiros termos de uma progressão geométrica (PG) de razão 3 é igual a 60, e a soma dos quatro primeiros termos de uma progressão aritmética (PA) também vale 60. Sabe-se que o primeiro termo da PA é igual ao primeiro termo da PG. A razão da PA é:
a) -3
b) 3/2
c) 3
d) 2/3
e) 9
Esse exercício envolve um pouco de PA – Progressão Geométrica – mas é muito bom. Vamos escrever a PG em função do seu primeiro termo, depois somamos os quatro primeiros termos e igualamos a 60. Resolvendo esse problema, calculamos o 1º termo da PG. O 1° termo da PG é igual ao 1º termo da PA, logo já sabemos o valor do 1º termo da PA. Vamos somar os 4 primeiros termos da PA e igualar a 60. Resolvendo esse problema encontramos a razão da PA. Vejam:
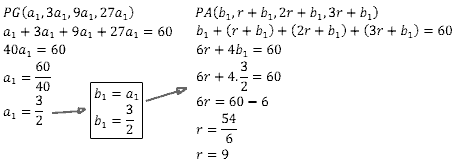
Exercício 6 – (Fuvest 2012) Considere uma progressão aritmética cujos três primeiros termos são dados por a1 = 1 + x, a2 = 6x, a3 = 2x² + 4 em que x é um número real. Determine os possíveis valores de x.
Vamos usar o mesmo princípio utilizado no exercício 2. a2-a1=a3-a2. A maior dificuldade nesse exercício vai ser resolver a equação do 2º grau.


Exercício 7 – (ITA/2000) O valor de n que torna a sequência (2 + 3n; –5n; 1 – 4n) uma progressão aritmética pertence ao intervalo:
a) [– 2, –1]
b) [– 1, 0]
c) [0, 1]
d) [1, 2]
e) [2, 3]
O raciocínio para resolver esse exercício é o mesmo dos exercícios 2 e 6.
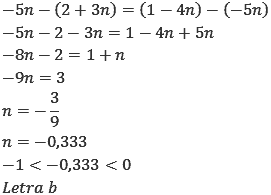
Exercício 8 – (UFG-GO) Sabendo-se que o quinto e o oitavo termo de uma PA crescente são as raízes da equação x²-14x+40=0, qual o terceiro termo dessa PA?
Para resolver esse exercício é indispensável saber calcular equação do 2º grau. O primeiro passo é resolver a equação do 2º grau. Vou resolver utilizando soma e produto.
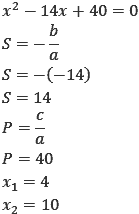
Concluímos que, por se tratar de uma PA crescente, o 5º termo da PA é 4 e o 8º termo é 10. Agora vamos escrever a PA em função da razão e calcular a razão e o 3º termo.
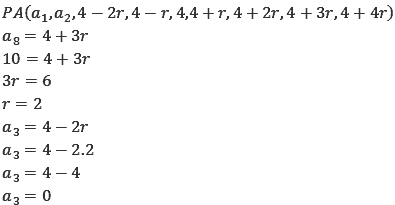
Exercício 9 – (PUC-SP) As quantias em reais de cinco pessoas estão em progressão aritmética. Se a segunda e a quinta possuem, respectivamente, R$250,00 e R$400,00, quanto a primeira possui?
Vamos escrever a PA em função da razão e dos valores conhecidos. Observem que é parecido com o exercício anterior.
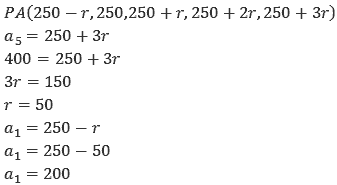
Vamos escrever a PA em função da razão e dos valores conhecidos. Observem que é parecido com o exercício anterior.
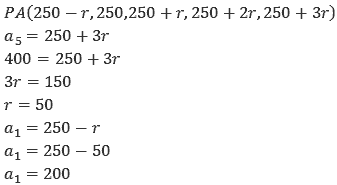

Comentários