Prova resolvida
Olá caros alunos e interessados! Como foram na prova da ESA? Vejam aqui as questões de Matemática do Exame Intelectual aplicado em 29 de julho de 2018.
ESA – 2018) Considere o número complexo z = 2 + 2i. Dessa forma, z100 :
(A) é um número imaginário puro.
(B) é um número real positivo.
(C) é um número real negativo.
(D) tem módulo igual a 1.
(E) tem argumento
(A) é um número imaginário puro.
(B) é um número real positivo.
(C) é um número real negativo.
(D) tem módulo igual a 1.
(E) tem argumento
Resolução:

Perceba que trata-se de um número real negativo.
Resposta: C
ESA – 2018) Lembrando que zero ou raiz da função f (x) = ax + b é o valor de x que torna a função nula, então, identifique a alternativa que apresenta a função f (x) cuja raiz é igual a + 3.
(A) f(x) = 2x – 5.
(B) f(x) = x + 3.
(C) f(x) = 3x.
(D) f(x) = x – 3.
(E) f(x) = 3x – 3
Resolução:

Resposta: D
ESA – 2018) Se a velocidade de um automóvel for aumentada em 60%, o tempo necessário para percorrer um mesmo trajeto, supondo a velocidade constante, diminuirá em:
(A) 30%.
(B) 40%.
(C) 37,5%.
(D) 62,5%.
(E) 60%.
Resolução:
Imagine que determinado automóvel percorre um trajeto a uma velocidade V km/h em T horas. Então Para calcularmos o tempo em que esse mesmo automóvel percorre o mesmo trajeto, ao aumentar sua velocidade em 60%, pode ser esquematizado pela seguinte proporção:
V ———— T
(1 + 60%).V ———- t
Repare que quanto MAIOR for a velocidade MENOR será tempo de percurso. Assim, velocidade e tempo são grandezas inversamente proporcionais, isto é:
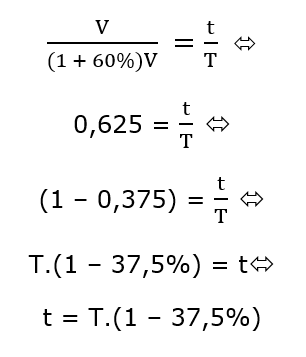
Repare que, em relação ao tempo original, o novo tempo equivale a uma redução de 37,5%.
Resposta: C
ESA – 2018)Seja a função definida por f: R → R, tal que f(x) = 2x . Então f(a + 1) – f(a) é igual a:
(A) f(1).
(B) 1.
(C) f(a).
(D) 2.f(a).
(E) 2
(A) f(1).
(B) 1.
(C) f(a).
(D) 2.f(a).
(E) 2
Resolução:

Resposta: C

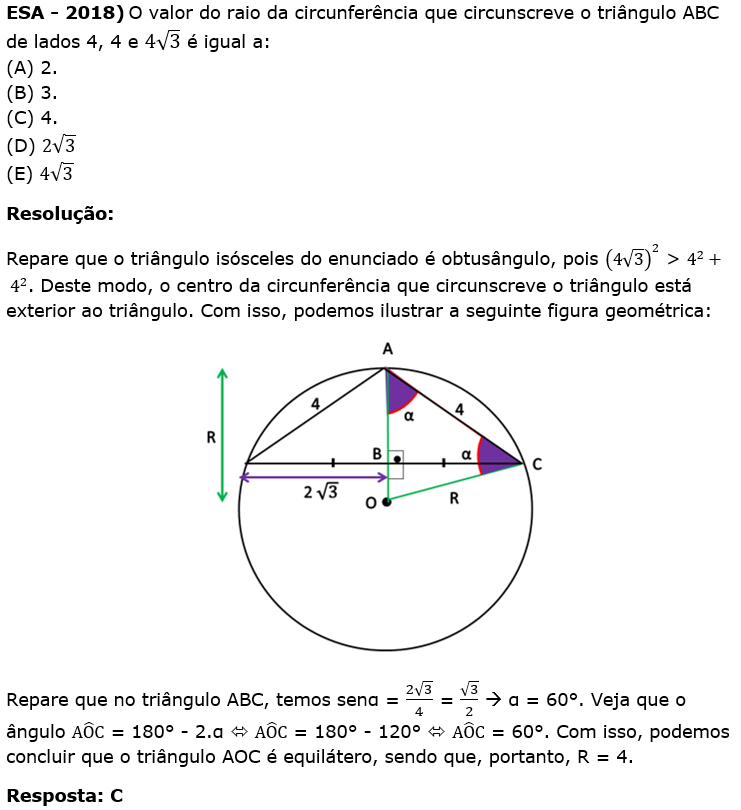
ESA – 2018)Em uma escola com 180 estudantes, sabe-se que todos os estudantes leem pelo menos um livro. Foi feita uma pesquisa e ficou apurado que:
50 alunos leem somente o livro A.
30 alunos leem somente o livro B.
40 alunos leem somente o livro C.
25 alunos leem os livros A e C.
40 alunos leem os livros A e B.
25 alunos leem os livros B e C.
Logo, a quantidade de alunos que leem os livros A, B e C é:
(A) 15.
(B) 20.
(C) 30.
(D) 25.
(E) 10.
50 alunos leem somente o livro A.
30 alunos leem somente o livro B.
40 alunos leem somente o livro C.
25 alunos leem os livros A e C.
40 alunos leem os livros A e B.
25 alunos leem os livros B e C.
Logo, a quantidade de alunos que leem os livros A, B e C é:
(A) 15.
(B) 20.
(C) 30.
(D) 25.
(E) 10.
Resolução:
Com os dados do enunciado, podemos construir o seguinte diagrama de Wenn:



ESA – 2018) Em uma Progressão Aritmética, o décimo termo vale 16 e o nono termo é 6 unidades maior do que o quinto termo.
Logo, o décimo segundo termo vale:
(A) 16,5.
(B) 19,5.
(C) 19,0.
(D) 17,0.
(E) 17,5.
Logo, o décimo segundo termo vale:
(A) 16,5.
(B) 19,5.
(C) 19,0.
(D) 17,0.
(E) 17,5.
Resposta:

Resposta: C
ESA – 2018)Em uma barraca de cachorro quente, o freguês pode escolher um entre três tipos de pães, uma entre quatro tipos de salsichas e um entre cinco tipos de molhos. Identifique a qualidade de cachorros quentes diferentes que podem ser feitos.
(A) 60.
(B) 86.
(C) 27.
(D) 12.
(E) 35.
(A) 60.
(B) 86.
(C) 27.
(D) 12.
(E) 35.
Resolução:
Repare que temos três tipos de pães, quatro tipos de salsichas e cinco tipos de molhos. Ou seja:
Para encontrar a quantidade de trios que compõe o cachorro quente, basta aplicarmos o princípio multiplicativo, pois assim, podemos obter a quantidade máxima de cachorros quentes diferentes que podem ser feitos. Ou seja:
3 x 4 x 5 = 60
Resposta: A
FONTE:

Comentários