Vetores Física Exercícios Resolvidos Ensino Médio
EXERCÍCIOS COM RESOLUÇÃO
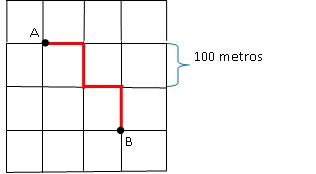
Numa cidade do interior de São Paulo, um novo bairro foi planejado para que todos os quarteirões sejam quadrados e suas ruas paralelas. A distância entre um par de ruas será de 100 m. Imagine um pedestre que realiza o percurso mostrado na figura, começando no ponto A e terminando sua trajetória no ponto B. Qual o módulo do vetor que representa a deslocamento (deslocamento vetorial) do pedestre?
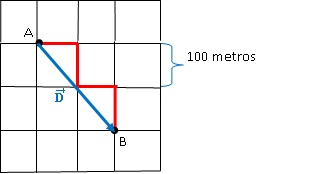
Para resolver esse problema, devemos lembrar a sobre trajetória e deslocamento. A trajetória é o que está traçado na figura, já o deslocamento é uma linha reta entre o ponto inicial e o ponto final. Esse então pode ser desenhado como um vetor: o vetor deslocamento representado na próxima figura.
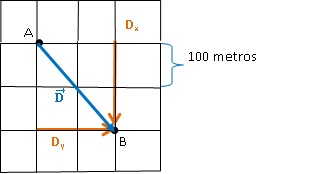
Para calcular o módulo precisamos ter os valores do comprimento dos componentes do vetor, neste caso chamado de Dx e Dy. Pelo gráfico podemos ver que Dx= 200 metros e Dy= 200 metros.
Assim módulo do vetor deslocamento é:
Observe que pela figura inicial, também podemos dizer qual foi o distância percorrida (trajetória) pelo pedestre, foi de 400 metros.Fonte: Objetos Educacionais.
Vetores
O Vetor é representado por uma seta. Esta seta representa uma grandeza vetorial, isto é, que tem módulo, direção e sentido.
Adição de Vetores
A soma de vetores pode ser feita por diversas maneiras, desde usando o Teorema de Pitágoras até utilizando a Regra do Polígono ou a Regra do Paralelogramo.
A soma de vetores pode ser feita por diversas maneiras, desde usando o Teorema de Pitágoras até utilizando a Regra do Polígono ou a Regra do Paralelogramo.
Teorema de Pitágoras
Exemplo: Uma pessoa anda 4 metros em direção ao norte e 3 em direção ao leste, quantos metros ela andou? Em que direção?
Regra do Polígono
A regra do polígono aplica-se colocando o início do vetor B no fim do vetor A, e assim consequentemente, até o final, tendo a figura, calcula-se o resultado.
Exemplo:
Uma pessoa anda dez metros para o norte e dois para o leste, a seguir, anda 2 metros para o sul e mais 4 para o leste. Qual o total de metros ela andou? Para qual direção?
A regra do polígono aplica-se colocando o início do vetor B no fim do vetor A, e assim consequentemente, até o final, tendo a figura, calcula-se o resultado.
Exemplo:
Uma pessoa anda dez metros para o norte e dois para o leste, a seguir, anda 2 metros para o sul e mais 4 para o leste. Qual o total de metros ela andou? Para qual direção?
Regra do Paralelogramo
A regra do Paralelogramo consiste em unir o ponto de inicio dos vetores e calcular a partir da equação abaixo o valor resultante:
A regra do Paralelogramo consiste em unir o ponto de inicio dos vetores e calcular a partir da equação abaixo o valor resultante:
Exemplo:
Um carro percorre 6 km para o sul e 8 km para o sudoeste. Sabendo que o sudoeste forma com o sul um ângulo de 45 graus, quantos km e em que direção o carro percorreu?

Um carro percorre 6 km para o sul e 8 km para o sudoeste. Sabendo que o sudoeste forma com o sul um ângulo de 45 graus, quantos km e em que direção o carro percorreu?
Ele percorreu 12,9m para o Sul-sudeste (SSE)
Revisando
Vetor: é um segmento de reta que tem que ter uma orientação.

Características de um Vetor:
• Módulo: é o tamanho do vetor.
• Direção: horizontal, vertical e inclinada.
• Sentido: é representado pela reta.
Vetor: é um segmento de reta que tem que ter uma orientação.
Características de um Vetor:
• Módulo: é o tamanho do vetor.
• Direção: horizontal, vertical e inclinada.
• Sentido: é representado pela reta.
Regra do paralelogramo
• Determina a direção e o sentido do vetor soma.
Teorema de Pitágoras
• Determina o módulo do vetor soma.
Regra de polígono
• Também determina a direção e o sentido do vetor soma.
Lei dos cossenos
• Determina o módulo do vetor soma.
cos 120º = -cos 60º
cos 150º = -cos 30º
cos 100º = -cos 80
• Determina a direção e o sentido do vetor soma.
Teorema de Pitágoras
• Determina o módulo do vetor soma.
Regra de polígono
• Também determina a direção e o sentido do vetor soma.
Lei dos cossenos
• Determina o módulo do vetor soma.
cos 120º = -cos 60º
cos 150º = -cos 30º
cos 100º = -cos 80
Vetores
• É a representação gráfica de uma grandeza vetorial (módulo, direção e sentido);
• Grandeza escalar – só precisa de módulo (é o valor numérico não negativo e a unidade);
• Grandeza vetorial – para ser bem definida precisa-se de módulo, direção e sentido;

• É a representação gráfica de uma grandeza vetorial (módulo, direção e sentido);
• Grandeza escalar – só precisa de módulo (é o valor numérico não negativo e a unidade);
• Grandeza vetorial – para ser bem definida precisa-se de módulo, direção e sentido;
Regra do Paralelogramo

Determinação do módulo do vetor
Mesma direção e sentidos opostos:

Ortogonais:

Mesma direção e sentidos opostos:
Ortogonais:
Vetor Oposto

Produto de um número real por um vetor

Subtração Vetorial

Produto de um número real por um vetor
Subtração Vetorial
Revisão de Matemática: Vetores
Vetores – Exercícios
01. Um projétil é lançado com uma velocidade de módulo 20 m/s e formando com o plano horizontal um ângulo de 60°. Calcule os componentes horizontal e vertical da velocidade.
02. INATEL) Dois corpos A e B se deslocam segundo trajetória perpendiculares, com velocidades constantes, conforme está ilustrado na figura adiante.
As velocidades dos corpos medidas por um observador fixo têm intensidades iguais a: VA = 5,0 (m/s) e VB = 12 (m/s). Quanto mede a velocidade do corpo A em relação ao corpo B?
03. (UnB) São grandezas escalares todas as quantidades físicas a seguir, EXCETO:
a) massa do átomo de hidrogênio;
b) intervalo de tempo entre dois eclipses solares;
c) peso de um corpo;
d) densidade de uma liga de ferro;
e) n.d.a.
04. (UEPG – PR) Quando dizemos que a velocidade de uma bola é de 20 m/s, horizontal e para a direita, estamos definindo a velocidade como uma grandeza:
a) escalar
b) algébrica
c) linear
d) vetorial
e) n.d.a.
05. (UFAL) Considere as grandezas físicas:
I. Velocidade
II. Temperatura
III. Quantidade de movimento
IV. Deslocamento
V. Força
Destas, a grandeza escalar é:
a) I
b) II
c) III
d) IV
e) V
06. (CESGRANRIO) Das grandezas citadas nas opções a seguir assinale aquela que é de natureza vetorial:
a) pressão
b) força eletromotriz
c) corrente elétrica
d) campo elétrico
e) trabalho
07. (FESP) Num corpo estão aplicadas apenas duas forças de intensidades 12N e 8,0N. Uma possível intensidade da resultante será:
a) 22N
b) 3,0N
c) 10N
d) zero
e) 21N
08. (FUND. CARLOS CHAGAS) O módulo da resultante de duas forças de módulos F1 = 6kgf e F2 = 8kgf que formam entre si um ângulo de 90 graus vale:
a) 2kgf
b) 10kgf
c) 14kgf
d) 28kgf
e) 100kgf
09. (UFAL) Uma partícula está sob ação das forças coplanares conforme o esquema abaixo. A resultante delas é uma força, de intensidade, em N, igual a:
a) 110
b) 70
c) 60
d) 50
e) 30
10. (ACAFE) Os módulos das forças representadas na figura são F1 = 30N, F2 = 20 N e F3 = 10N. Determine o módulo da força resultante:
a) 14,2 N
b) 18,6 N
c) 25,0 N
d) 21,3 N
e) 28,1 N
Leia o artigo: Cálculo Vetorial
Respostas:
01 – Vx = 10m/s
02 – 13 m/s
03 – C 04 – D 05 – B 06 – D
07 – C 08 – B 09 – D 10 – D
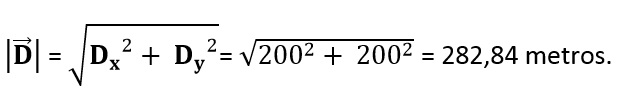
Comentários